A printer-friendly version of this document is available as a PDF file (80 kbytes).
Electric field for point-like charges
These notes are a wrapped-up version of the problem solved in the tutorial.
The problem: Assume you have three charges on the x-axis; from left to right they are. The distances between consecutive charges is
(see the diagram for details).
Task: find the point(s) on the x-axis at which the electric field vanishes.
Let us try to figure out, on a diagram, in which
regions on x-axis one may hope to find a point of ![]() .
In what follows
.
In what follows ![]() and
and ![]() will be used partially interchangeable;
I hope this will not create confusion. Anyway, in our case
on the x-axis one has
will be used partially interchangeable;
I hope this will not create confusion. Anyway, in our case
on the x-axis one has
![]() ,
so the magnitude
,
so the magnitude ![]() of
of ![]() is the absolute value of
is the absolute value of ![]() .
.
On the top of the diagram, in three rows,
the ![]() 's generated by each of
the charges is depicted.
As you can see, the field created by
's generated by each of
the charges is depicted.
As you can see, the field created by ![]() is pointing toward the charge in all of the regions. The
field created by the positive charges is ``outbound'' from
the corresponding charge. To add some information,
the magnitudes of the vectors are also indicated.
The
fields are calculated at the middle point of each interval,
that is at
is pointing toward the charge in all of the regions. The
field created by the positive charges is ``outbound'' from
the corresponding charge. To add some information,
the magnitudes of the vectors are also indicated.
The
fields are calculated at the middle point of each interval,
that is at ![]() of the adjacent charges.
I also indicated the fields at the points which are
at
of the adjacent charges.
I also indicated the fields at the points which are
at ![]() to the left of
to the left of ![]() and to the right of
and to the right of ![]() .
The numbers on the arrows are the relative magnitudes
of the fields - the unit magnitude is the value
of
.
The numbers on the arrows are the relative magnitudes
of the fields - the unit magnitude is the value
of ![]() generated by the
generated by the ![]() at distance
at distance ![]() around it1
around it1
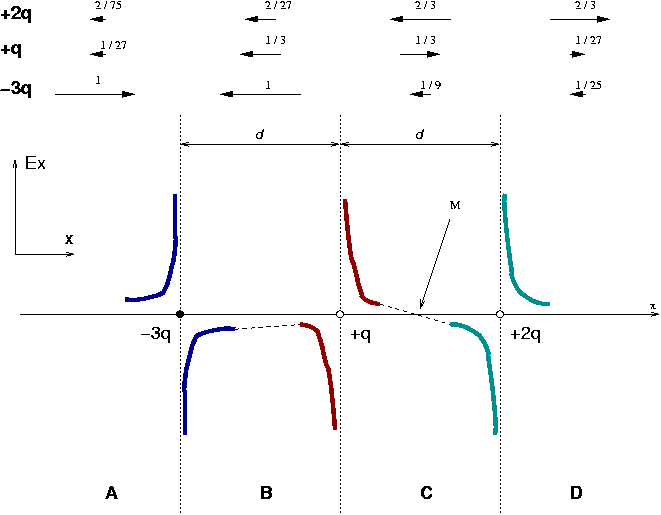
As one may notice, in region B the fields are all oriented in the same direction, to the left, therefore we should not expect the resultant field to vanish in that region. May we expect to find solutions in all other regions?
To check this, let us sketch the behaviour of the
resultant ![]() in the vicinity of the charges.
It is clear that close to a charge, the value
of the field is mainly due to the charge sitting at that
particular location. For example,
at the point located at distance
in the vicinity of the charges.
It is clear that close to a charge, the value
of the field is mainly due to the charge sitting at that
particular location. For example,
at the point located at distance ![]() to the left of the
to the left of the
![]() charge, the projection on x-axis of the total field
is given by2
charge, the projection on x-axis of the total field
is given by2
Since the value of the field is a continuous function of distance
(except for the location of the charges, where ones gets singularities),
we observe that in region C
there must be a point M at which ![]() .
.
What about regions A and D? The field apparently goes to 0 at large distances away from the charges. It can be shown that it is not vanishing at any finite distance in those regions. The proof is postponed to the end of this document. In conclusion, there is only one point of x-axis at which the field vanishes.
To find the position of M we choose the origin of the
x-axis to be at the location of the ![]() charge. Let the
coordinate of M be
charge. Let the
coordinate of M be ![]() . Then the distances from M to
the
. Then the distances from M to
the ![]() and
and ![]() charges are
charges are ![]() and
and ![]() , respectively.
, respectively.
The field ![]() on x-axis
has only
on x-axis
has only ![]() component. We require
component. We require
Let us now prove that the field does not vanish in the A and D regions. In the textbook (Serway & Jewett) there is a similar problem, 19.15, dealing with the field generated by a dipole on its axis.
As before, we choose the origin of x-axis at the location
of ![]() charge, and find the expression for
charge, and find the expression for ![]() far away from
the charges, say, in the region D. Let
far away from
the charges, say, in the region D. Let ![]() denote
the position at which we calculate the field. For this
situation we assume
denote
the position at which we calculate the field. For this
situation we assume ![]() , which is to say that
, which is to say that
![$\displaystyle k_e\left[- \frac{3q}{(x+d)^2}
+ \frac{q}{x^2}
+ \frac{2q}{(x-d)^2}\right]$](img30.png) |
|||
![$\displaystyle \frac{k_e q}{x^2}\left[
- \frac{3}{(1+\xi)^2}
+ 1
+ \frac{2}{(1-\xi)^2}\right]$](img31.png) |
|||
![$\displaystyle \frac{k_e q}{x^2}\left[
- 3(1-2\xi)
+ 1
+ 2(1+2\xi)\right]$](img33.png) |
|||
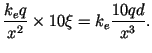 |
(4) |
Revised: 02/06/05 © 2005 Sorin Codoban
Created on