S P A R C Stratospheric Processes And their Role in Climate A project of the World Climate Research Programme Home Initiatives Organisation Publications Meetings Acronyms and Abbreviations Useful Links

Stratosphere-Troposphere Coupling

Peter Haynes, Department of Applied Mathematics and Theoretical Physics, Cambridge, UK (phh@damtp.cam.ac.uk)

Introduction

It is widely accepted that the troposphere has a strong dynamical effect on the stratosphere, primarily through the upward propagation of waves, both
low-frequency large-scale Rossby waves (‘planetary waves’) and high-frequency inertia-gravity waves. Understanding of this effect is based on simple theories of wave propagation (including the wellknown Charney-Drazin criterion for vertical Rossby wave propagation), experiments in many different types of numerical models, plus observational indicators such as differences in stratospheric circulation between summer and winter, and between the hemispheres. An important aspect of this effect is that in the stratosphere there is a two-way interaction between waves and mean flow. Breaking or
dissipating waves exert a systematic mean force G that changes the mean flow. The mean flow, on the other hand, affects the propagation, breaking and dissipation of waves and hence itself affects G . The twoway interaction can lead, for example, to sensitivity to initial conditions, or to internal
dynamical variability. Yoden et al. (2002) and Haynes (2005) review some these issues.

Nonetheless, it is still not yet the case that our understanding of the dynamical effect of the troposphere on the stratosphere can be said to be complete. For example, for events such as stratospheric sudden warmings (including the unexpected Southern Hemisphere sudden warming of September 2002), in which the stratospheric circulation is highly perturbed, it does not seem possible to identify unambiguously anomalously large tropospheric wave
forcing as the cause. (See for example papers in the recent special issue of Journal of Atmospheric Sciences, volume 62, number 3.) One of the reasons may be that the view of the troposphere having a one-way dynamical effect on the stratosphere is seriously limited. There are plenty of reasons why the coupling should be two-way. The large-scale extratropical dynamics of the atmosphere is inherently non-local in both horizontal and vertical. Changes in the stratosphere must inevitably affect the troposphere and vice versa – the key question, of course, is how much?

Stratospheric cause and tropospheric effect?

The dynamical effect of the stratosphere on the troposphere is now a major research activity. (See previous SPARC newsletter articles by Gillett et al. 2003, Hartmann 2004.) Whilst there has for some time been significant evidence from numerical model studies, early examples being Boville
(1984) and Kodera et al. (1990), that imposed perturbations to the stratosphere lead to changes in the tropospheric circulation and that the mechanism for communication of these changes is dynamical, much of the recent heightened interest in this topic has arisen from studies of the Northern Hemisphere (NH) and Southern Hemisphere (SH) ‘annular modes’ (hereafter NAM and SAM). Methods such as EOF analysis have identified these as dominant
signals in variability in both troposphere (e.g. Thompson and Wallace 2000 and references therein) and stratosphere (e.g. Baldwin and Dunkerton 1999). In both troposphere and stratosphere, the annular modes are associated with variation in the strength and position of the jet (the mid-latitude jet in the troposphere, the polar night jet in the stratosphere). However the underlying dynamical character of the modes is somewhat different in the two cases.

In the troposphere the annular mode variability is believed to arise from two-way interaction between baroclinic eddies and the tropospheric mid-latitude jet (e.g. Robinson 1991, Feldstein and Lee 1998, Hartmann and Lo 1998). In the stratosphere, on the other hand, the annular variability is a manifestation of the variation in the strength of the polar-night jet, driven by the wave force G . A significant ingredient is the variability in tropospheric wave forcing, although as noted earlier, there is an important role for two-way interaction between waves and mean flow here too.

What has caused widespread interest is that there seem to be strong correlations between the annular mode variability in the troposphere and that in the stratosphere. For example, in NH winter there is significant correlation between the annular mode index defined on the basis of the surface pressure
field and the stratospheric circulation, so that when there is a strong pole-to-equator pressure gradient at the surface, indicating strong eastward surface flow, there are also strong eastward winds throughout the midlatitude troposphere and in the mid-to-high latitude stratosphere (Thompson and Wallace, 2000). There is corresponding organisation in the wave fluxes indicating propagation and momentum transport, both in the troposphere (Limpasuvan and
Hartmann 2000) (as is expected from the accepted mechanism for the variability) and also in the stratosphere (Hartmann et al. 2000) (see Figure 1) implying corresponding differences in the wave force G .

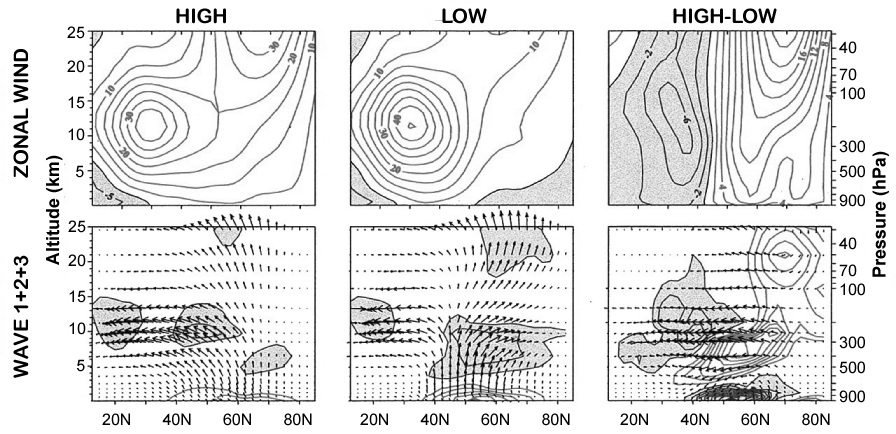Figure 1: (From Hartmann et al. 2000.) Composites for periods of high and low NAM index and their difference (left, centre and right, respectively) in longitudinal wind (top) and Eliassen-Palm flux, which indicates wave propagation and transport of westward momentum, and its divergence, which indicates eastward wave force. Positive contours are grey, negative contours black, with negative regions shaded. The Eliassen-Palm flux is calculated only for longitudinal wavenumbers 1, 2 and 3. In the ‘high’ phase wave fluxes tend to be directed equatorward within the troposphere and to converge in the subtropical troposphere, whereas in the ‘low’ phase wave fluxes tend to be directed upward from troposphere to stratosphere and to converge, implying an anomalous westward wave force, in the mid- and high latitude stratosphere. For better resolution, please contact the SPARC Office.

Baldwin and Dunkerton (1999, 2001) have shown that the vertical structure of NAM variation in NH winter typically shows a downward propagation from middle stratosphere to troposphere and the corresponding figure from their 2001 paper is now (quite justifiably) de rigeur in any scientific talk in this area. Does this picture imply a direct effect, with some delay, of anomalies in the stratospheric circulation in mid-stratosphere on the troposphere?

The answer is ‘not necessarily’. The equatorial quasi-biennial oscillation (QBO) is an educational example. The QBO is manifested by downward propagating anomalies in zonal wind, however it was pointed out by Plumb (1977) that, at least in simple dynamical models of the QBO, there is in
fact no downward propagation of information. The evolution of the flow below some given level is completely independent of any changes that are made above that level. The distinction in elementary wave theory between phase propagation on the one hand, and group propagation on the other,
with only the latter unambiguously associated with propagation of information, is well-known. The downward propagation of wind anomalies in the QBO can be seen as a sort of phase propagation.

Simple dynamical models of the equatorial QBO of the type studied by Plumb (1977) are not necessarily relevant to the extratropical stratosphere, in particular because rotation is omitted and because a WKBJ approximation is used in calculating the structure of the waves for given mean flow. However
Plumb and Semeniuk (2003) have shown in a simple wavemean model of the extratropical stratosphere (that does incorporate rotation and uses a
weaker approximation for the spatial structure of the waves) that forcing at low levels can give rise in the stratosphere above to downward propagating
structures similar to those observed by Baldwin and Dunkerton. Therefore, such structures do not necessarily imply downward propagation of information.

There is similar uncertainty in interpretation of the correlations between anomalies of zonal velocities and wave fluxes of the type shown by Hartmann et al.
(2000), (Figure 1), for example. While these correlations strongly suggest dynamical connections between troposphere and stratosphere involving two-way interactions between mean flow and waves, it is impossible to tell from the correlations alone whether there is an effect of the stratosphere on the troposphere, or the troposphere on the stratosphere (or indeed whether it makes sense only to think of the troposphere-stratosphere system as intrinsically coupled, with the whole idea of the effect of one component on the other as intrinsically flawed).

Notwithstanding the above, there are now many examples of simulations in numerical models where changes in the troposphere have been shown to result from imposed changes in the stratosphere. In these cases downward propagation of information is difficult to discount. Some relevant examples include imposed perturbations to the upper stratosphere (Kodera et al. 1990,Gray 2003) as a simple representation of solar cycle effects, changes to stratospheric radiative equilibrum temperature profiles in a simplified general circulation model (Polvani and Kushner 2002, Kushner and Polvani 2004), changes to Southern Hemisphere stratospheric ozone in a general circulation model (Gillett and Thompson 2003) and changes to stratospheric initial conditions in a numerical weather prediction model (Charlton et al. 2004). The results of Scott and Polvani (2004), obtained in a simplied dynamical model with a
damped troposphere, show nicely that the wave flux from troposphere to stratosphere cannot be considered to be set by the tropospheric wave forcing alone and that the stratosphere can to some extent determine how much wave flux it accepts.

Dynamical mechanisms

There are several possible dynamical mechanisms by which the stratosphere might affect the troposphere. There are two aspects to this: (a) how information might be communicated in the vertical and (b) why the tropospheric response might be larger than expected. Figure 2 is a schematic diagram indicating some of the points discussed below.

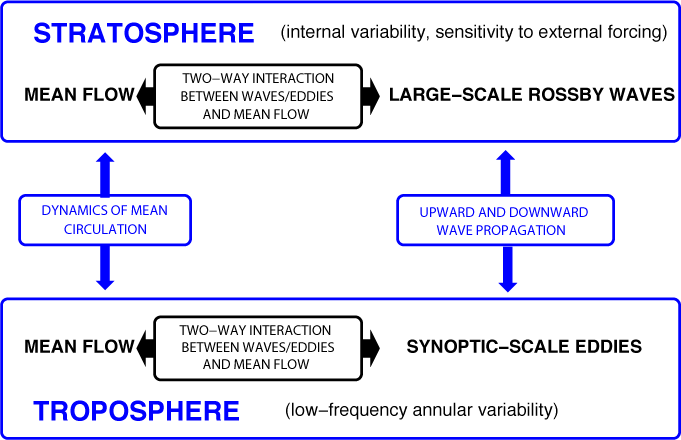Figure 2: Schematic diagram indicating the role of different aspects of the dynamics in the dynamical mechanisms discussed in the text. Note that ‘dynamics of mean circulation’ includes non-local PV inversion (or equivalently the short-time effect of the meridional circulation) and the effect of the meridional circulation on longer time scales, including the ‘downward control’ limit. (Copyright 2000, Natl. Acad. Sci, U.S.A. Reproduced with permission.) For better resolution, please contact the SPARC Office.

Taking (a) first, one mechanism is via the non-local inversion operator that determines quantities such as velocity or temperature from the potential vorticity (PV) distribution. (The non-locality arises from the rapid propagation of inertio-gravity waves required to maintain a state of geostrophic and hydrostatic balance.) Any change in the PV distribution in the lower stratosphere will inevitably give rise to changes in wind and temperature in the troposphere. Hartley et al. (1998), Ambaum and Hoskins (2002) and Black (2002) show explicit calculations to illustrate this point. This might account for some of the lower part of the height-time plots shown by Baldwin and Dunkerton (1999, 2001). If the restriction is made to zonal mean fields, then the vertical nonlocality
of PV inversion is precisely equivalent to a statement that a wave-induced force localised to the stratosphere will, through the instantaneous induced meridional circulation, give rise to an acceleration in the troposphere below and many of the papers on this topic have chosen the latter description. An important refinement is that on longer timescales, in the presence of radiative damping, the meridional circulation tends to be narrower and deeper below (Haynes et al. 1991, Holton et al. 1995) (tending to a ‘downward control’ response in the steady state limit) potentially allowing an enhanced tropospheric response to a stratospheric wave force.

A second distinct mechanism for communication in the vertical is via Rossby wave propagation. The propagation of Rossby waves out of the troposphere might be sensitive to by variation in the ‘refractive’ properties of the lower stratospheric flow (Hartmann et al., 2000, see also Limpasuvan and Hartman 2000), or indeed there might be downward reflection of Rossby waves from higher in the stratosphere (e.g. Perlwitz and Harnik 2003, 2004).

A third mechanism for downward propagation of information might be through a two-way interaction between waves and mean flow. The results of Plumb and Semeniuk (2003) discussed earlier do not completely rule out the possibility that there can be real downward propagation of information through this interaction. Recent investigation (Steven Hardiman, personal communication) using the same model as Plumb and Semeniuk has shown no evidence of any distinct downward propagation of the effect of imposed upper level stratospheric perturbations through a such a mechanism when stratospheric Rossby wave amplitudes are weak. When stratospheric wave amplitudes are large, however, the dynamics of waves and mean flow is highly nonlinear and imposed upper level perturbations can have significant effects at lower levels.

Turning to (b), the two-way interaction between baroclinic waves and mean flow in the troposphere that gives rise to annular mode variability may also serve as an ‘amplifier’ for external forcing (including dynamical forcing from the stratosphere) (e.g.Hartmann et al. 2000). This may allow the tropospheric response to be significantly larger than might be expected from zonal-mean dynamics, for example.

Putting (a) and (b) together Song and Robinson (2004) report numerical experiments showing the effect of imposed stratospheric perturbations on the troposphere and the effect arises through a downward penetrating response in the mean circulation communicates the effect of stratospheric wave forcing to the troposphere, where the response is amplified by the eddy (i.e. wave) feedbacks associated with annular variability. They name their mechanism ‘downward control with eddy feedback’. However, having proposed this mechanism (which to this author at least seemed interesting and plausible) Song and Robinson then present further numerical experiments that show that it cannot be the full explanation for the effect of stratospheric perturbations on tropospheric circulation that they observe. In particular they show that the effect on the tropospheric circulation is much weaker when the Rossby waves in the stratosphere are artificially damped. The conclusion is therefore that the Rossby waves play a significant role in downward communication of information.

Other strong evidence that the stratosphere plays an active, rather than a passive, role in tropospheric variations associated with the NAM comes from observed and modelled changes on the time scale of the NAM variations. Baldwin et al. (2003) have shown that this time scale is significantly
longer at times of the year (NH winter, SH spring) when there is strong Rossby wave propagation into the stratosphere. Correspondingly, artificial suppression of stratospheric variability in model simulations reduces the time scale of the tropospheric NAM (Norton 2003). The dynamical mechanism here is likely to be that, when there is significant flux of Rossby waves into the stratosphere, the flow in the stratosphere acts as an integrator (and hence low-pass-filter) of this flux (or rather the variability in this flux), since stratospheric damping times are relatively long. Any stratospheric effect on the troposphere will therefore tend to increase the time scales of the variability. When there is little flux of Rossby waves into the stratosphere (in summer, or in SH midwinter) the effect is absent.

Conclusion

The possibility of significant stratospheric effects on the troposphere has implications for many aspects of month-to-month and year-to-year variability and systematic change in the tropospheric circulation. It suggests possible mechanisms for explaining apparent signals in the tropospheric circulation of the solar cycle, inputs of volcanic aerosol to the stratosphere, and the equatorial QBO. It also strengthens the link between between possible climate change
in the troposphere and changes in the stratosphere, due to ozone depletion or increasing greenhouse gases.Whilst care is needed in interpreting observations as implying real downward influence or downward propagation, there is convincing evidence from numerical model simulations that changes in the stratosphere can sometimes lead to significant effects in the troposphere.

The dynamical mechanisms required to explain these effects are still being investigated. It seems clear that the two-way interaction between synoptic-scale waves/eddies and mean flow in the troposphere that gives rise to ‘annular variability’ is important, notwithstanding the fact that the nature of annular variability is still being vigorously debated (e.g. Cash et al. 2005). The two-way interaction between waves and mean flow in the stratosphere also seems likely to be relevant, though the relative roles of waves, mean flow, and coupling between them is not yet clear.

Further clarification of these dynamical mechanisms and their role in the real atmosphere will most likely come from careful studies in a sequence of numerical models. Much has already been learned from simplified models that include the large-scale dynamics plus highly simplified representations of processes such as radiation, and more work with these models, as well as with sophisticated general circulation models, is surely needed to resolve
some of the remaining uncertainties.

An important general point that has been revived by the recent interest in troposphere-stratosphere coupling is that, whether or not one is interested in the dynamical details, the fact is that the coupled system exhibits strong (dynamical) internal variability and that any attempt to explore correlations between one part of the atmosphere and the other, or to predict future changes, needs to take this into account. Such studies therefore need to use long integrations or large ensembles, requiring significant computational resources. There is understandable pressure to make as rapid progress as possible with coupled chemical-climate simulations, which also requires significant computational resources, but there is still much to learn about the variability and predictability of the coupled physics and dynamics of troposphere- stratosphere system without coupling to chemistry, and this should not be overlooked.

References

Ambaum, M. H. P., and B. J. Hoskins, 2002. The NAO troposphere-stratosphere connection. J. Climate, 15:1969–78.

Baldwin M. P., and T. J. Dunkerton, 1999. Propagation of the Arctic Oscillation from the stratosphere to the troposphere. J. Geophys. Res., 104:30937-46.

Baldwin M. P., and T. J. Dunkerton, 2001. Stratospheric harbingers of anomalous weather regimes. Science 294:581-84.

Baldwin M. P., D. B. Stephenson, D. W. J. Thompson, T. J. Dunkerton, A. J. Charlton, and A. O’Neill, 2003. Stratospheric memory and skill of extended-range weather forecasts. Science, 301:636-40.

Black R. X., 2002. Stratospheric forcing of surface climate in the Arctic Oscillation. J. Climate, 15:268–77.

Boville B. A., 1984. The influence of the polar night jet on the tropospheric circulation in a GCM. J. Atmos. Sci., 41: 1132–1142.

Cash B. A., P. J. Kushner, and G. K. Vallis, 2005. Zonal asymmetries, teleconnections and annular patterns in a GCM. J. Atmos. Sci., 62: 207–219.

Charlton A. J., A. O’Neill,W. A. Lahoz, and A. C. Massacand, 2004. Sensitivity of tropospheric forecasts to stratospheric initial conditions. Quart. J. Roy. Met. Soc., 130: 1771-1792.

Feldstein S., and S. Lee, 1998. Is the atmospheric zonal index driven by an eddy feedback? J. Atmos. Sci., 55:3077-86.

Gillett N. P., M. P. Baldwin, D.W. J. Thompson, E. F. Shuckburgh, W. A. Norton, and J. L. Neu, 2003. Report on the SPARC workshop on the
role of the stratosphere in tropospheric climate. SPARC Newsletter 21: 7-9.

Gillett, N. P., and D. W. J. Thompson, 2003. Simulation of recent Southern Hemisphere climate change. Science, 302: 273-275.

Gray, L. J., 2003. The influence of the equatorial upper stratosphere on stratospheric sudden warmings. Geophys. Res. Lett., 30: 1166.

Hartley,D. E., J. T.Villarin, R. X. Black, and C. A. Davis, 1998. A new perspective on the dynamical link between the stratosphere and troposphere.
Nature, 391:471–74.

Hartmann, D. L., 2004. The stratosphere in the climate system. SPARC Newsletter 22: 15-18.

Hartmann, D. L., and F. Lo, 1998. Wave-driven zonal flow vacillation in the Southern Hemisphere. J. Atmos. Sci., 55:1303-15.

Hartmann, D. L., J. M.Wallace, V. Limpasuvan, D.W. J. Thompson, and J. R. Holton, 2000. Can ozone depletion and global warming interact to
produce rapid climate change?. Proc. Nat. Acad. Sci. (Wash. DC), 97:1412–17.

Haynes, P.H., 2005. Stratospheric dynamics. Ann. Rev. Fluid Mech., 37:263-293. Haynes, P. H., C. J.Marks, M. E.McIntyre, T. G. Shepherd, and K. P. Shine, 1991. On the “downward control” of extratropical diabatic circulations by eddy-induced mean zonal forces. J. Atmos. Sci., 48: 651–78.

Holton, J. R., P. H. Haynes, and M. E. McIntyre, A. R. Douglass, R. B. Rood, and L. Pfister, 1995. Stratosphere–troposphere exchange. Revs.
Geophys., 33:403–39.

Kodera, K., K. Yamazaki, K. Chiba, and K. Shibata, 1990. Downward propagation of upper stratospheric mean zonal wind perturbation to the troposphere. Geophys. Res. Lett., 17:1263-66.

Kushner, P. J., and L. M. Polvani, 2004. Stratosphere-troposphere coupling in a relatively simple AGCM: the role of eddies. J. Climate, 17: 629-639.

Limpasuvan, V., and D. L. Hartmann, 2000. Wave-maintained annular modes of climate variability. J. Climate, 13:4414-29.

Norton, W. A., 2003. Sensitivity of northern hemisphere surface climate to simulation of the stratospheric polar vortex. Geophys. Res. Lett. 30:1627.

Perlwitz, J., and N. Harnik, 2003. Observational evidence of a stratospheric influence on the troposphere by planetary wave reflection. J. Climate, 16:3011-26.

Perlwitz, J., and N. Harnik, 2004. Downward coupling between the stratosphere and the troposphere: the relative roles of wave and zonal mean processes. J. Climate, 17:4902-4909.

Plumb, R. A., 1977. The interaction of two internal waves with the mean flow: implications for the theory of the quasi-biennial oscillation. J. Atmos. Sci., 34:1847–58.

Plumb, R. A., and K. Semeniuk, 2003. Downward migration of extratropical zonal wind anomalies. J. Geophys. Res., 108: 4223, doi:10.1029/2002JD002773.

Polvani, L. M., and P. J. Kushner, 2002. Tropospheric response to stratospheric perturbations in a relatively simple general circulation model. Geophys. Res. Lett,. 29: 1114, doi:10.1029/2001GL014284.

Robinson, W. A., 1991. The dynamics of the zonal index in a simple model of the atmosphere. Tellus, 43A:295–305.

Scott, R. K., and L. M. Polvani, 2004. Stratospheric control of upward wave flux near the tropopause. Geophys. Res. Lett., 31:doi:10.1029/2003GL017965.

Song, Y., and W. A. Robinson, 2004. Dynamical mechanisms of stratospheric influences on the troposphere. J. Atmos. Sci., 61:1711-25.

Thompson, D. W. J., and J. M. Wallace, 2000. Annular modes in the extratropical circulation. Part I: Month-to-month variability. J. Climate, 13:1000-16.

Yoden, S., M. Taguchi, and Y. Naito, 2002. Numerical studies on time variations of the troposphere- stratosphere coupled system. J. Met. Soc. Japan, 80:811–830.

TOP