S P A R C Stratospheric Processes And their Role in Climate A project of the World Climate Research Programme Home Initiatives Organisation Publications Meetings Acronyms and Abbreviations Useful Links

Temperatures, Transport, and Chemistry in the TTL

Ian Folkins , Dalhousie University, Halifax, Canada (Ian.Folkins@dal.ca)

The Tropical Tropopause Layer (TTL) has been recently introduced (Highwood and Hoskins, 1998, Folkins et al., 1999) as a layer whose properties
are intermediate between the troposphere and stratosphere. If examined with a fine enough spatial scale, any atmospheric property will vary continuously in going from one atmospheric layer to the next. One could therefore invoke the existence of a transition layer between any two adjacent atmospheric layers. This article will attempt to explain what is unique about the TTL, and why it provides conceptual advantages in thinking about some atmospheric
science problems.

The issue of how to define the TTL is not settled. Here, the base of the TTL will be defined as the Level of Zero clear sky radiative Heating (LZH), which occurs near 15 km. The transition from radiative cooling (below 15 km) to radiative heating (above 15 km) is driven by the combination of a rapid decrease in water vapour mixing rations (such that longwave cooling from water vapour is negligible above 15 km), and also by the onset of extremely cold temperatures, which suppress longwave emission from CO2 and O3. From radiative considerations, an air parcel which detrains from a deep convective clouds above the LZH will rise upward across isentropic surfaces into the stratosphere. This definition of the base of the TTL therefore seems to be
the definition most relevant to stratosphere- troposphere exchange (STE). Air parcels that detrain into the TTL have some probability of influencing the chemical composition of the stratosphere, while those which detrain below the TTL have very little. It should be kept in mind, however, that air parcels moving horizontally near 15 km will roughly follow an isentropic surface that can undulate above and below 15 km, so that the base of the TTL is
not a material surface. Perhaps the most reasonable definition of the base of the TTL is the height at which an air parcel detraining from a deep convective cloud first attains a 50% likelihood of ascending into the stratosphere. This height probably occurs near the LZH because radiative heating is the most dominant diabatic process in the clear sky atmosphere.

It is more difficult to define the top of the TTL. A useful conceptual definition is that it is the height at which the upward convective mass flux becomes small in comparison to the Brewer Dobson mass flux. That is, that the convective outflow that feeds the base of the Brewer Dobson circulation has essentially
become exhausted. Unfortunately, it is intrinsically difficult to diagnose the high altitude tail of the convective detrainment profile from observations. Measurements of ozone and other chemical species suggest that undiluted convective outflow can occur as high as 17 km (Folkins et al., 2002a, Tuck
et al., 2004), which would place the top of the TTL near the climatological height of the cold point tropopause. This is also a convenient definition for TTL dehydration. However, deep convective overshooting through the tropical tropopause, followed by mixing with ambient stratospheric air, provides a mechanism for convective detrainment above 17 km whose existence is difficult to detect from chemical tracers.

It has been argued that the input of significant amounts of overshooting tropospheric air above the tropical tropopause is unlikely, since it would undermine the seasonal variation in CO2 propagating upward from the tropopause (Boering et al., 1995). Model simulations suggest, however, that this is not true in all circumstances (Sherwood and Dessler, 2003).

As defined here, the TTL is a consequence of the geometry of the flow in the upper tropical troposphere. In order to feed the Brewer-Dobson circulation, there must be some convective detrainment above the altitude at which the background mean flow changes direction. Since the Brewer-Dobson circulation is about 100 times smaller than the Hadley circulation, one would anticipate that roughly 1% of the mass flux from tropical deep convection detrains into the TTL.

Figure 1 gives an overview of the mass flux divergences in the upper tropical troposphere associated with convective outflow ( c), radiative cooling ( r), and evaporative cooling ( e). These were obtained using a simple one-dimensional model of the tropical atmosphere constrained by observed temperature and moisture profiles (Folkins and Martin, 2005). To first order, radiative convergence balances convective divergence. In other words, convective outflow is the mass source required to supply a downwardly increasing subsiding radiative mass flux (or to supply an upwardly increasing ascending radiative mass flux in the TTL).

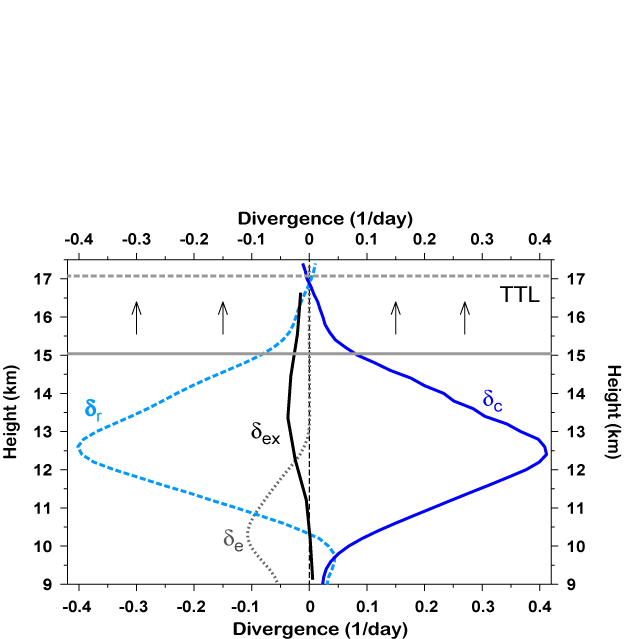Figure 1:  Tropical mean (20°S – 20°N) mass flux divergences calculated from a one-dimensional model of the tropical atmosphere (Folkins and Martin, 2005).  dc refers to the convective divergence, dr to the radiative divergence, de to the evaporative divergence, and dex to the divergence associated with export of tropical air into the extratropics.  The vertical arrows indicate that the clear sky mass flux is upward above 15 km.  The top of the TTL, near 17 km, has been drawn with a dashed line to indicate that its height is uncertain. For better resolution, please contact the SPARC Office.

The magnitude of the evaporative driven downward mass flux increases below 13 km, giving rise to a convergence, which partially balances the divergence from convection. Due to the extremely cold temperatures, saturated water vapour mixing ratios in the TTL are very low, typically less that 10 ppmv.
At such low mixing ratios, heat releases associated with changes in phase of water are typically smaller than those due to radiative heating or cooling, so that from a thermodynamic perspective, air parcels in the TTL can be effectively treated as dry. In the TTL, one should not ordinarily have to worry about the role of evaporating ice crystal in driving vertical motions.

Figure 1 shows that the rate at which deep convection injects air into the upper tropical troposphere reaches a maximum of 0.4/day near 12.5 km. The convective replacement time r can be defined as r=1/ c. This replacement time varies from 2.5 days at the peak of deep outflow mode, to about two weeks at the base of the TTL. Within the TTL, estimations of c and r using simple models become highly uncertain. This is due to a variety of reasons. The divergences shown in Figure 1 were calculated by assuming that the mass budget of the tropics (here defined as 20°S-20°N) could be treated in isolation from the extratropics. This assumption is probably valid at most heights. In the TTL, however, it is likely that the rate of mass transfer between the tropics and extratropics is comparable with the convective divergence. The curve labelled ex in Figure 1 is an estimate of the rate at which tropical air is exported from the tropics to the extratropics, using assimilated meteorological data from the Goddard Earth Observing System (GEOS) of the NASA Data Assimilation Office. In principle, diagnostic approaches to estimating the strength of the convective divergence in the TTL should take this mass transport pathway into account. In addition, the radiative divergence shown in Figure 1 was calculated by assuming clear sky conditions. Clear sky heating rates in the TTL are very small. The relative importance of cloud radiative effects can therefore be expected to be much higher in the TTL than in the rest of the tropical troposphere.

The ideas behind the TTL are not entirely new. Until recently, however, there had been a widely held implicit assumption that much of the air rising in deep convective clouds detrained near, or just below, the tropical tropopause. This view partly arose from the fact that stratiform anvil clouds from deep convection frequently extend to the cold point tropopause (~17 km). Inferring mass outflow from the presence of ice crystals is, however, problematic. Ice crystals may arise from vertical motions associated with gravity waves generated by convection, rather than by the updrafts themselves. In addition, stratiform anvils can extend from 10 km to 17 km. There is no reason to assume a priori that outflow is preferentially distributed near cloud top.

Temperature profiles from radiosondes also frequently give the impression of a strong convective influence extending up to the cold point tropopause. Deep convection is often associated with a cold and well-defined cold point tropopause, with layers near the tropopause where the lapse rate approaches the dry adiabatic value. The strong influence of deep convection of TTL temperatures does not necessarily imply rapid mass outflow rates in the TTL, however, since the weakness of radiative heating rates in the TTL implies long radiative damping timescales (Hartmann et al., 2001). Temperature anomalies in the TTL arising from deep convection can be therefore expected to be very persistent.

The notion that most of the air transported upward in deep convective clouds reaches the tropical tropopause also gives rise to an apparent thermodynamic paradox. In the absence of mixing, the level of neutral buoyancy of an air parcel rising upward inside a convective updraft occurs at the height at which the equivalent potential temperature of the air parcel is equal to the potential temperature of the background atmosphere. (This statement makes a number of assumptions, among them that water vapour concentrations are sufficiently low that their effect on density can be ignored, and that the presence of condensate does not have an appreciable effect on the density of an air parcel.) While the potential temperature at the cold point tropopause is rarely lower than 365 K, near surface air parcels with e > 365 K are extremely rare (Folkins and Martin, 2005). On thermodynamic grounds, one would therefore also expect convective detrainment near the cold point tropopause to be extremely rare.

There have been a number of attempts to reconcile the idea of significant convective detrainment near the tropical tropopause with its apparent thermodynamic implausibility. One mechanism that would allow air parcels to detrain at a higher potential temperature surface is convective overshooting and irreversible mixing. It has also been pointed out that the potential temperature of the cold point tropopause roughly corresponds to the saturated equivalent potential temperature of the warmest tropical sea surface temperatures, so that air parcels with e ~ 365 K can in fact be generated near the surface (Chimonas and Rossi, 1987). Another suggestion is that the freezing of lofted ice could act as a source of heating that would allow air parcels to detrain near the tropical tropopause (Zipser, 2003). Such estimates are, however, quite sensitive to assumptions on the amount of lofted ice, and the efficiency with which rising air parcels retain this additional heat.

Both simple diagnostic models, as well as in situ chemical evidence, indicate that outflow from deep convective clouds ranges from 10 km to 17 km. This suggests that approaches that attempt to relate a mean detrainment potential temperature to a mean boundary layer e may be misguided. Instead, it may be more appropriate to attempt to find some relationship between the shape of the deep convective detrainment profile in the upper troposphere with
the probability distribution of boundary layer e in actively convecting regions (Folkins and Martin, 2005).

The mean profile of any chemical tracer in the tropics should reflect an approximate balance between the competing tendencies of in situ chemistry, vertical advection, convective detrainment, as well as other possible influences such as STE. In the vicinity of the 12.5 km c maximum, chemical tracers with upper tropospheric lifetime longer than a week should be maintained near their boundary layer values by the strength of deep convective detrainment. However, as the timescale for convective replacement increases toward the cold-point tropopause, the mean concentration of a chemical tracer can be expected
to become increasingly determined by in situ chemistry.

Figure 2 (see colour insert II) shows ozone climatologies at ten tropical locations from the SHADOZ campaign (Thompson et al., 2003). Most of these profiles exhibit the classic “S-shape”.The minimum near 12.5 km is probably due to the strong convective outflow at this altitude. Ozone mixing ratios at
locations characterized by maritime deep convection are smaller than those with continental deep convection. The two dashed lines are ozone profiles calculated from a model forced by the convective divergence profile shown in Figure 1 (Folkins and Martin, 2005). In one of the profiles, the
mean ozone mixing ratio in air detraining from convective clouds is assumed to be 20 ppbv, while in the other, it is assumed to be 30 ppbv. In the model, the increase in ozone mixing ratios above 13 km is due to the increase in the convective replacement timescale, which allows ozone to approach its steady state mixing ratio. The increase in ozone above 13 km is not driven by an increase in the rate of in situ chemical production from O2 photolysis. This source of ozone is insignificant below 16.5 km.

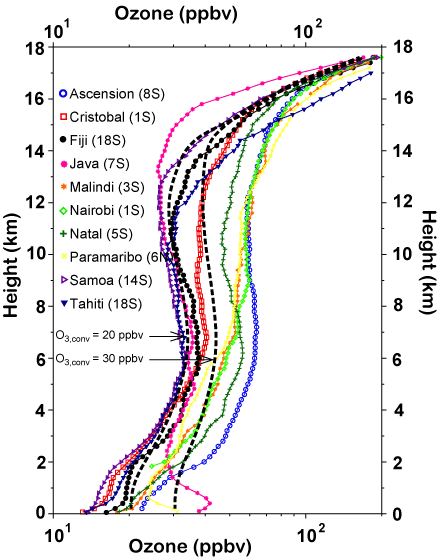Figure 2:  The profiles shown in grey are ozone climatologies using data from SHADOZ ozonesonde stations between 20°S and 20°N.  The dashed lines refer to ozone profiles generated by a one-dimensional model (Folkins and Martin, 2005) with different values of O3,conv.  O3,conv refers to the mean ozone mixing ratio of air parcles detraining from convective clouds. For better resolution, please contact the SPARC Office.

Figure 3 show profiles of CO in the tropics obtained from various field campaigns. Unfortunately, there are far fewer measurements of CO than O3 in the tropics, especially between DC8 (~11 km) and ER-2 flight altitudes (15 km to 20 km). None of the CO profiles shown in Figure 3 contain enough
data to constitute a climatology. CO is primarily destroyed in the upper troposphere by OH attack. Since the sources of CO are mainly at the surface, one would expect deep convection to maintain high concentrations of CO near the 12.5 km convective outflow maximum, and decrease toward the tropopause as the convective source weakened. This expectation is broadly consistent with the CO profiles shown in Figure 3.

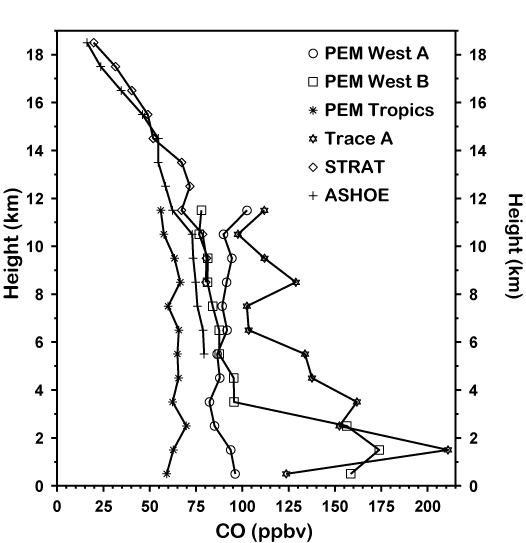Figure 3:  CO climatologies obtained by averaging over CO measurements (15°S – 15°N) from a variety of aircraft field campaigns. For better resolution, please contact the SPARC Office.

One would also expect tracers, which are influenced by STE to exhibit a vertical gradient in the upper tropical troposphere. It has been noted that the onset of a decrease in CFC-11 sometimes occurs below the tropical tropopause (Tuck, 1997). This was attributed to the existence of a “standing reserve” of stratospheric air in the upper tropical troposphere. The existence of such a reservoir of stratospheric air in the TTL is consistent with Figure 1, which suggests that the timescales for sideways tropicalextratropical exchange and deep convection in the TTL may be comparable. In these cases, the vertical gradient in the tracer concentration is not necessarily caused by a change in the magnitude of STE with height, but by a decrease in convective outflow, which gives any stratospheric input a longer chemical signature.

The base of the TTL denotes a change in the nature of the clear sky water vapour budget. In most of the clear sky tropical troposphere, the occurrence of supersaturation with respect to ice is inhibited by large-scale descent. In the TTL, however, air parcels experience colder temperatures as they ascend toward the cold point tropopause. Supersaturation with respect to ice should be quite frequent, provided ice deposition nuclei are sufficiently rare. Measurements have, in fact, suggested an increase in the frequency of clear sky supersaturation at the base of the TTL (Folkins et al., 2002b). These measurements would tend to support the view that dehydration occurs throughout the TTL rather than simply in the vicinity of the cold point tropopause. Unambiguous detection of clear sky supersaturation with respect to ice remains a significant experimental challenge, however, because in regions where the relative humidity approaches 100%, it is possible to observe supersaturation with respect to ice simply due to the existence of random (and possibly bias) errors in measurements of water vapour mixing ratio and temperature.

The concept of the TTL was partly motivated by modelling studies indicating that convective control of tropical temperatures did not extend as high as the cold point tropopause (Thuburn and Craig, 2002). It is clear that the base of the TTL is associated with a change in the nature of radiativeconvective equilibrium. Figure 4 (see colour insert III) shows the difference in December to February (DJF) temperatures at 14 tropical radiosondes locations from a DJF climatology obtained by averaging over all 14 locations. Below 14 -15 km, locations characterized by persistent deep convection tend to be anomalously warm, while those with less convection tend to be anomalously cold.

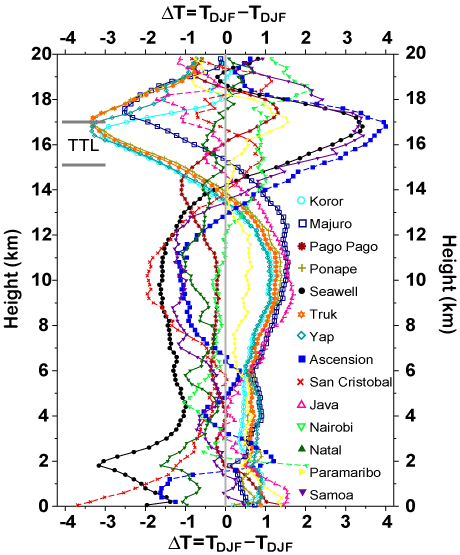Figure 4:  The vertical variation of seasonal temperature anomalies in the tropics.  DT=TDJF - TDJF where TDJF is the December-January-February climatology at each radiosonde station, and TDJF refers to the average of TDJF over all 14 radiosonde stations. For better resolution, please contact the SPARC Office.

One of the ways in which convection influences the large scale temperature profile is by the emission of gravity waves. These gravity waves give rise to irreversible vertical motions in the background atmosphere, which diminish the contrast in density between the atmosphere and the convective plumes (Bretherton and Smolarkiewicz, 1989). A warm positively buoyant plume would be expected to give rise to downward motions in the background atmosphere, while a negatively buoyant plume (overshooting updraft or downdraft) would give rise to upward motions. The association between convection and warm anomalies below the TTL would suggest that convective plumes are on average positively buoyant below 15 km, while the association between convection and cold anomalies in the TTL would suggest that convective plumes in this region are negatively buoyant.

The coincidence of the LZH with the height at which the relationship between convective frequency and temperature changes sign is coincident with the view that deep convection exerts a dominant control on temperature at these altitudes. Below the TTL, the induced downward motions from deep convection increase tropical temperatures away from radiative equilibrium, and give rise to radiative cooling, which within the TTL, the induced upward motions from deep convection decrease tropical temperatures away from radiative equilibrium, and give rise to radiative heating.

There have been other explanations put forward for the association between cold temperatures and deep convection in the TTL. One possibility is that it is due to the deep convection injection of cold, negatively buoyant air which irreversibly mixes with the ambient warmer air (Sherwood et al., 2003, Kuang and Bretherton, 2004).

In the lower tropical stratosphere, upwelling is strongest during the December to Febraury (DJF) season and weakest during the June to August (JJA) season. This is associated with a seasonal temperature cycle, in which temperatures are coldest during the DJF season and warmest during the JJA season. Figure 5 (see colour insert III) shows the difference between the JJA and DJF seasonal temperature climatologies at 14 radiosonde locations. The amplitude of the lower stratospheric seasonal cycle peaks near 18 km. At most locations, the onset of this seasonal cycle occurs near 15 km, so that the stratospheric seasonal cycle extends to the base of the TTL. Below 15 km, most tropical locations are warmer during the DJF season.

Predictions of the future evolution of tropical cold point temperatures are made difficult both by uncertainty in the mechanism by which tropical deep convection influences TTL temperatures, and also because the relative roles played by the Hadley and Brewer-Dobson circulations in controlling TTL temperatures have not yet been established. It is important to determine the nature of this control, however, because the Hadley and Brewer Dobson
circulations can be expected to change in response to future changes in CO2. By influencing tropical cold point temperatures, these changes can be expected to influence stratospheric water vapour.

Ozone plays an important role in the radiative budget of the TTL. Its climatological profile will be influenced by changes in both the shape of the convective detrainment profile, and by changes in stratospheric upwelling. It would therefore be desirable to investigate the future evolution of TTL temperatures using models in which the dynamics is self-consistently coupled with radiation and chemistry.

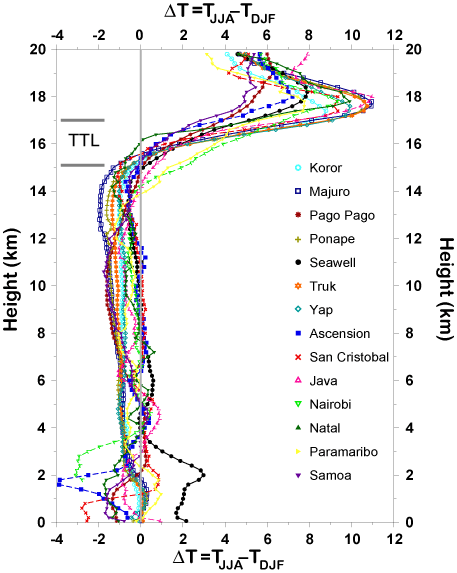Figure 5:  Vertical profiles of the difference between the mean JJA and DJF temperatures at various radiosonde locations.  The temperature difference is defined as DT=TJJA – TDJF. For better resolution, please contact the SPARC Office.

References

Boering, K. A., et al., Measurements of stratospheric carbon dioxide and water vapor at northern midlatitudes: Implications for troposphere- to-stratosphere transport, Geophys. Res. Lett., 22, 2737-2740, 1995.

Bretherton, C. S., and P. K. Smolarkiewicz, Gravity waves, compensating subsidence and detrainment around culmuls clouds, J. Atmos. Sci., 46, 740-759, 1989.

Chimonas, G., and R. Rossi, The relationship between tropopause potential temperature and the buoyant energy of storm air, J. Atmos. Sci.,44, 2902-2911, 1987.

Folkins, I., M. Lowewenstein, J. Podolske, S. Oltmans, and M. Proffitt, A barrier to vertical mixing at 14 km in the tropics: Evidence from ozonesondes and aircraft measurements, J. Geophys. Res.,104, 22095-22102, 1999.

Folkins, I., C. Braun, A. M. Thompson, and J. C. Witte, Tropical ozone as an indicator of deep convection, J. Geophys. Res., 107(D13), 10.1029/2001JD001178, 2002a.

Folkins, I., E. J. Hintsa, K. K. Kelly, and E. M. Weinstock, A simple explanation for the relative humidity increase between 11 and 15 km in
the tropics, J. Geophys. Res., 107, 10.1029/2002JD002185, 2002b.

Folkins, I., and R.Martin, The vertical structure of tropical convection, and its impact on the budgets of water vapor and ozone, to be published
in J. Atmos. Sci., 2005.

Hartmann, D. L., J. R. Holton, and Q. Fu, The heat balance of the tropical tropopause, cirrus, and stratospheric dehydration, Geophys. Res. Lett., 28, 1969-1972, 2001.

Highwood, E. J., and B. J. Hoskins, The tropical tropopause, Q. J. R. Meteorol. Soc., 124, 1579- 1604, 1998.

Kuang, Z., and C. S. Bretherton, Convective influence of the heat balance of the tropical tropopause layer: A cloud-resolving model study. J. Atmos. Sci., 61, 2919-2927, 2004.

Sherwood, S. C., and A. E. Dessler, Convective mixing near the tropical tropopause: Insights from seasonal variations, J. Atmos. Sci., 60, 1847-1856, 2003.

Sherwood, S. C., T. Horinouchi, and H. A. Zeleznik, Convective impact on temperatures observed near the tropical tropopause, J. Atmos. Sci., 60, 1847-1856, 2003.

Thompson, A. M., et al., Southern Hemisphere Additional Ozonesondes (SHADOZ) 1998- 2000 tropical ozone climatology 1. Comparison with Total Ozone Mapping Spectrometer (TOMS) and ground-based measurements. J. Geophys. Res., 108, 8238, 10.1029/2001JD 000967, 2002.

Thuburn, J., and G. C. Craig, On the temperature structure of the tropical sub-stratosphere, J. Geophys. Res., 107, 10.1029/2001JD000448, 2002.

Tuck, A. F., et al., The Brewer Dobson circulation in the light of high altitude in situ aircraft observations. Q. J. R. Meteorol. Soc., 124, 1-70,
1997.

Tuck, A. F., et al., Horizontal variability 1-2 km below the tropical tropopause, J. Geophys. Res., 109, 10.1029/2003JD003942, 2004.

Zipser, E. J., Some views on “hot towers” after 50 years of tropical field programmes and two years of TRMM data. Meteorological Monographs, 29,
49-58, 2003.

TOP