3-source interference

A printer-friendly version of this text is available here (1 page, pdf).

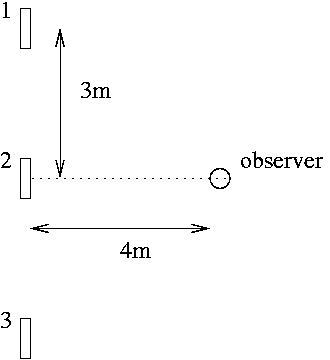
This is the solution to problem # 73 from Chapter 21 of the Knight textbook. The setup is depicted in the figure.

The wave produced by the top [1] and bottom [3] speakers at the location of the observer is

$$A_1 =A_3 = a \sin (5\pi -\omega t),$$ (1)

while speaker 2 produces a wave given by

$$A_2 = a \sin (4\pi -\omega t).$$ (2)

In this problem it is easier to just substitute the numerical values for distances and $k$ (- the wave number), rather than carry on the whole algebraic expression (... $\sin(kx-\omega t)$, etc.). Namely,

$$k = \frac{2\pi}{\lambda} = \frac{2\pi f}{v} = \frac{2\pi 170}{340} = \pi m^{-1}.$$

In (1) and (2) the coefficients 4 and 5 are just the distances from the speakers to the observation point ( $5 = \sqrt{3^2 +4^2}$ ). The resultant amplitude due to the superposition of the waves is

$$A = A_1 +A_2 + A_3 = 2 a \sin (5\pi -\omega t)+ a \sin (4\pi... ...ga t) = 2a \sin(\omega t) -a \sin(\omega t) = a\sin(\omega t).$$ (3)

The answer looks like an oscillation of amplitude $a$ - this is the answer for part a).

For part b) let us notice that the wavelength of the waves is $\lambda =v/f = 2m$. Waves from speakers 1 and 3 arrive at the observation point with a $5\pi$ phase shift (relative to the phase at the source) - this is due to the distance source-observer of 2.5 wavelengths, while the wave from speaker 2 arrives with a phase of $4\pi$ (2.0 wavelengths). Hence, it is obvious we need to shift speaker 2 to the left by 1.0$m$ (half of $\lambda$), so that the phase at arrival is also $5\pi$, and therefore constructive interference at the observation point. Note that we could have shifted speaker 2 to the right by 1.0$m$ with the same result (but they specifically asked us to move the speaker to the left).

For part c) the answer is straightforward - we use equation (3) but with $a \sin (4\pi -\omega t)$ replaced by $a \sin (5\pi -\omega t)$, and obtain

$$A^* = 3a \sin (5\pi -\omega t).$$

The intensity of the sound is proportional to the square of the amplitude of oscillation, so the answer for this part is that the sound intensity is 9 times greater under the constructive interference from the 3 speakers scenario, compared to the sound intensity from a single speaker.

As a final observation, please note that we assumed the amplitude of the wave from the 2-nd speaker to be still $a$ at the observation point, even after we shifted the speaker to the left! Well, is this reasonable ...? Perhaps not, but otherwise we don't get the answer from the textbook :-)

Last revised:November 29, 2006;      solution by Sorin Codoban.