A printer-friendly version of this document is available as a PDF file, 2 pages 100kbytes.
Projectile motion
These notes present the solution of the problem #43 from Ch. 3 of Serway&Jewett.
A projectile is launched up an incline (incline angle ![]() )
with an initial speed
)
with an initial speed ![]() at an angle
at an angle ![]() with respect
to the horizontal
with respect
to the horizontal
![]() ,
(see the setup on the right of Fig. 1).
,
(see the setup on the right of Fig. 1).
(a) Show that the projectile travels a distance ![]() up the incline,
where
up the incline,
where
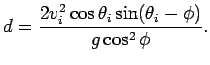
(b) For what value of ![]() is
is ![]() a maximum,
and what is that maximum value?
a maximum,
and what is that maximum value?
Review of the task: (a) to check that the distance along the incline
![]() is given by a certain formula, and (b)
to find the value of
is given by a certain formula, and (b)
to find the value of ![]() which, for a fixed
which, for a fixed ![]() , gives us the maximum value of the range
, gives us the maximum value of the range ![]() .
.
We write the kinematic equations the usual way.
For the case (I) we have
 |
(5) |
For the case (II) the equations of motion read
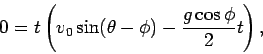 |
(8) |
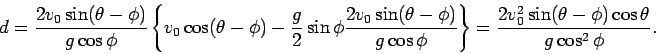 |
(10) |
Note: To get ![]() we didn't divide anywhere by expressions
which vanish when
we didn't divide anywhere by expressions
which vanish when ![]() . Hence, we expect that in the
limit
. Hence, we expect that in the
limit
![]() the expression for
the expression for ![]() recovers a known result for projectile motion
(e.g. find the range
for given initial
recovers a known result for projectile motion
(e.g. find the range
for given initial ![]() and angle
and angle ![]() with horizontal).
In our case, for
with horizontal).
In our case, for ![]() we get
we get
![]() , so the
check for a limiting case is passed.
, so the
check for a limiting case is passed.
To solve the part (b) we also have at least two choices.
One choice would be to take the derivative of ![]() with respect
to
with respect
to ![]() , while keeping
, while keeping ![]() constant, and
demand
constant, and
demand
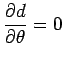 .
This will give us
.
This will give us ![]() for which
for which ![]() has an extremum or saddle point.
We need then to check that this extremum is indeed a maximum.
has an extremum or saddle point.
We need then to check that this extremum is indeed a maximum.
The other choice is to rewrite the expression for ![]() in
such a way that the answer becomes obvious. We will pursue this path.
in
such a way that the answer becomes obvious. We will pursue this path.
Let us note that for given ![]() (and kept constants)
the only factor in the expression for
(and kept constants)
the only factor in the expression for ![]() that depends on
that depends on ![]() is
is
![]() . This can be rewritten as (see footnote 1)
. This can be rewritten as (see footnote 1)
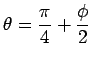 .
Using (11), the maximum value of
.
Using (11), the maximum value of
Last revised: September 25, 2003 © 2003, Sorin Codoban