A printer-friendly version of this document is available as a PDF, 2 pages, 70kbytes.

Free falling objects

These notes present the solution of the problem #52 from Ch. 2 of Serway&Jewett.

``A rock is dropped from rest into a well. (a) If the sound of the splash is heard $2.40s$ later, how far below the top of the well is the surface of the water? The speed of sound in air is $336m/s$. (b) If the travel time for the sound is ignored, what percentage error is introduced when the depth of the well is calculated?''

Figure 1: The setup.

Let us denote the total time by $\tau$ and the depth of the well by $H$ and take $g=9.80m/s^2$.

It is clear that the total time is the sum of the time of free fall $\tau_f$ plus the time $\tau_c$ it takes the sound to propagate ``back''. For the free fall we have

$$H=y=\frac{g}{2}\tau_f^2 \Rightarrow \tau_f=\sqrt{\frac{2H}{g}},$$ (1)

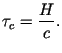while for the sound travel we get Hence, the total time is given by

$$\tau=\sqrt{\frac{2H}{g}}+ \frac{H}{c}.$$ (2)

We need to solve for $H$. From (2) one obtains

$$0< \sqrt{\frac{2H}{c}} = \left(\tau-\frac{H}{c}\right).$$ (3)

We outlined the positiveness of both sides for reasons to be explained in a moment. From (3) we derive a quadratic equation in $H$ with the solutions

$$H_{1,2} = c\left\{ \tau +\frac{c}{g} \pm\frac{c}{g}\sqrt{1+\frac{2g\tau}{c}}\right\}.$$ (4)

Interesting enough, both solutions in (4) are positive! Which solution should we choose?

The relief is brought by the equation (3) which implies $H<c\tau$. This condition rules out the ``$+$'' solution (please check for yourself!). We are left with

$$H = c\left\{ \tau +\frac{c}{g} - \frac{c}{g}\sqrt{1+\frac{2g\tau}{c}}\right\}.$$ (5)

Numerically, $H=26.4m$.

(b) If the travel time for sound is neglected the depth $\tilde{H}$ we estimate is

$$\tilde{H}=\frac{g}{2}\tau^2,$$ (6)

which numerically gives us $\tilde{H}= 28.2m$. Therefore, the percentage error is

$$\varepsilon = \frac{\tilde{H}-H}{H} = 0.068 = 6.8\%$$ (7)

One may ask how does this percentage error changes with the depth, or for that matter, with the time $\tau$ that we measure. In Fig. 2 the error $\varepsilon$ was plotted against the time $\tau$. We see that for $\tau=30s$ we get $\varepsilon=0.75$. Observe that I plotted only $\tau<33s$. If there is no friction then $33s$ is about the time when the speed of free fall equals the speed of sound; arguably, at this speed the formulae for subsonic fall cease to be valid :-)

Figure 2: The error $\varepsilon$ plotted vs. measured time $\tau$ (see text for details).

Last revised: September 25, 2003 © 2003 Sorin Codoban