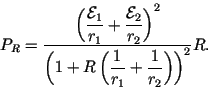A printer-friendly version of this document is
available as a PDF file (40 Kbytes).
Battery & resistor games
These notes are a wrapped-up version of the
problem solved in the tutorial.
It is a well known problem
in Physics and Engineering (although I don't have a precise reference
for it).
The problem:
Assume we have a DC circuit as the one sketched in Figure 1.
The battery has the EMF 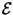 and internal resistance
and internal resistance
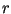 . The external resistor has resistance
. The external resistor has resistance 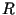 which can be varied
(from 0 to
which can be varied
(from 0 to 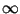 ).
The task: find the value of
).
The task: find the value of 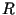 for which the power
for which the power 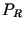 delivered to/dissipated on
delivered to/dissipated on 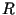 reaches its maximum.
reaches its maximum.
Figure 1:
Circuit diagram for one battery + resistor
|
|
To solve the problem we apply Kirchhoff's law for the loop.
We have
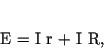 |
(1) |
where 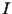 stands for the current through the circuit.
The power delivered to
stands for the current through the circuit.
The power delivered to 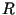 is given by
is given by
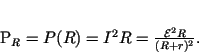 |
(2) |
At this point we can just simply take the derivative of
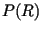 with respect to
with respect to 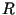 , set it to zero and solve for
, set it to zero and solve for 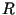 .
The function
.
The function 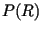 at the solution will
have an extremum; to check that we have a maximum we would
need to take the second derivative,
at the solution will
have an extremum; to check that we have a maximum we would
need to take the second derivative,
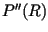 and see if it is
negative when evaluate at the ``suspect'' point.
and see if it is
negative when evaluate at the ``suspect'' point.
Figure 2:
A sketch of the 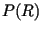 behaviour
behaviour
|
|
It would be a bit more educating to proceed at a slower pace, with
a bit less mathematics (at least at the beginning).
Let us first stare a bit at equation (2),
which is now rewritten in the form
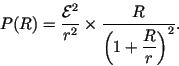 |
(3) |
Now it becomes obvious that for
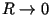 the expression
for
the expression
for 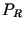 also goes to 0, and almost linearly (indeed, in the denominator
we have
also goes to 0, and almost linearly (indeed, in the denominator
we have
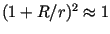 , hence
, hence 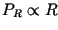 in this regime).
For
in this regime).
For
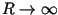 the picture is different, but
the picture is different, but
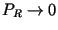 as well.
In this case the denominator may be approximated by
as well.
In this case the denominator may be approximated by 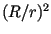 ; therefore, the
; therefore, the
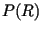 behaves like
behaves like
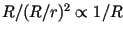 . The behaviour
of
. The behaviour
of 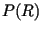 in both extreme cases
is sketched in Fig. 2. Clearly, there must be a value(s)
of
in both extreme cases
is sketched in Fig. 2. Clearly, there must be a value(s)
of 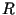 for which
for which 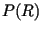 reaches maximum.
To find the value of
reaches maximum.
To find the value of 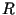 for which
for which 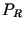 reaches the extremum
we still need to do the math.
The first derivative on ``the top of the hill'' has to vanish:
reaches the extremum
we still need to do the math.
The first derivative on ``the top of the hill'' has to vanish:
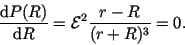 |
(4) |
The unique solution of the above equation is 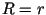 . To convince
yourself that this value provides a maximum for
. To convince
yourself that this value provides a maximum for 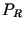 you have to take
the second derivative of
you have to take
the second derivative of 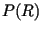 and check it is negative when
evaluated at
and check it is negative when
evaluated at 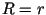 . This task is left to the reader.
For completeness, let us calculate the value of
. This task is left to the reader.
For completeness, let us calculate the value of 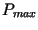 .
We have
.
We have
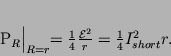 |
(5) |
Here 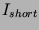 stands for the shortcircuit current - this is the
maximum current the battery can deliver.
One may complicate the problem by considering (see Fig. 3)
two batteries
connected in parallel and delivering power to a (variable) resistor
stands for the shortcircuit current - this is the
maximum current the battery can deliver.
One may complicate the problem by considering (see Fig. 3)
two batteries
connected in parallel and delivering power to a (variable) resistor 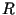 .
The reader is again advised to perform the same task: find the condition
.
The reader is again advised to perform the same task: find the condition
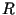 should obey for the power dissipated on it to reach its maximum.
As an incentive here is the answer for the power:
should obey for the power dissipated on it to reach its maximum.
As an incentive here is the answer for the power:
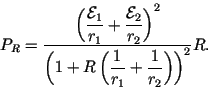 |
(6) |
The power is maximum when
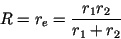 |
(7) |
and the expression for the maximum power is similar to
(5), with 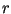 being replaced by
being replaced by 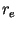 and
and 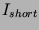 being now the sum of the shortcircuit currents.
being now the sum of the shortcircuit currents.
Figure 3:
The circuit for the 2 batteries + resistor case
|
|
Last revised: 02/07/05 Written by Sorin Codoban
Created on
2005-10-31
![]() and internal resistance
and internal resistance
![]() . The external resistor has resistance
. The external resistor has resistance ![]() which can be varied
(from 0 to
which can be varied
(from 0 to ![]() ).
The task: find the value of
).
The task: find the value of ![]() for which the power
for which the power ![]() delivered to/dissipated on
delivered to/dissipated on ![]() reaches its maximum.
reaches its maximum.