Previous: Introduction Next: Advection Using Real Wind Data Up: Ext. Abst.
A model of a two-dimensional nondivergent flow on a rotating sphere
with forcing and dissipation is considered following Ishioka and
Yoden (1995). The system is governed by a vorticity equation:
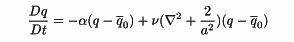
where q is the PV (or, the absolute vorticity in this case), and
over-bar denotes zonal mean. The first term on the right hand
side is a relaxation term to a prescribed zonally symmetric forcing
defined below. with the relaxation time of ± = 10 days. The second
term is an artificial small viscosity with ? = 6.43 x 104 m2 s-1.
A spectral model with T85 truncation and the 4th-order Runge-Kutta
method is used for time integrations with a time increment of
1/80 day. We use the analytic form of the forcing originally introduced
by Hartmann (1983):
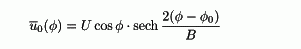
where U, B, and Æ0 are parameters characterizing the polar-night jet; U is a measure
of intensity of the jet, B its width, and Æ0 its position. It is converted to forcing of PV in the vorticity
equation.
We use two parameter sets, (U, Æ0, B) = (180 m s-1, 50°, 15°) and (180 m s-1, 50°, 10°) . While these parameter sets are close to each other, the solutions are categorized into different regimes (Ishioka and Yoden 1995): the former parameter set gives a quasi-periodic solution, and the latter gives an aperiodic one. After the initial transient period, the flow settles into a state in which the forcing to intensify the unstable jet and the disturbances growing from the barotropic instability are balanced. We investigate the flow after 1000-day integration. And trajectories are computed simultaneously with the time integration of the flow field.
Finite-time Lyapunov exponent gives the exponential growth rate of the distance between two nearby trajectories. It depends on initial position and evaluation time. Figure 1 shows the spatial distributions of the largest finite-time Lyapunov exponents for the quasi-periodic solution (a,b) and the aperiodic solution (c,d) for two evaluation times of Ä=2 and 90 days. Calculations are done on every 2° x 2° grid in the latitudes of Æ > 20° with two small perturbations of angular length of 10-6rad in longitudinal and latitudinal directions. Linear deformation effect due to horizontal shear appears in the both results of Ä=2 days (a,c) because of the short evaluation time. Low value is seen on a ring corresponding to the edge of the polar vortex. High value is seen in the both flanks of the jet, particularly in the equator side. The effect by chaotic behavior of the particles is not clear at this stage. For longer time intervals, the exponent shows stronger dependence on the initial position, since Lagrangian behavior is chaotic. In the quasi-periodic flow, the ring of low value is well identified even for Ä=90 days at the edge of the polar vortex (b). The edge of the polar vortex is less evident (d) in the aperiodic solution, but the value inside is lower than outside, which is consistent with previous studies (e.g. Bowman 1993; Bowman and Chen 1994). Spatial distributions for the both solutions show large inhomogeneity inside the polar vortex. A large triangular region with round corners in which the value is very low is seen inside the vortex. The region is still discernible in the both solutions even Ä=90 days. In addition, a croissant-shape region with low exponent is also seen between the triangular region and the vortex edge, particularly in the quasi-periodic solution.
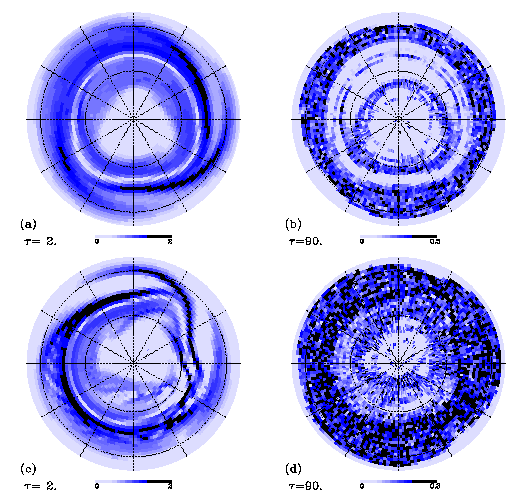
Fig.1 Distributions of the largest finite-time Lyapunov exponent on all grid of 2 degrees for the quasi-periodic solution (a,b) and the aperiodic solution (c,d).
In the quasi-periodic flow, Poincare sections are available in this co-rotating frame with the vortex Trajectories of several particles are calculated for a long integration time, and the positions at every one vacillation cycle are all plotted on one figure. Figure 2 shows the Poincare sections computed for 1000 vacillation cycles with 12 particles initially put outside the polar vortex (a), and 19 particles inside the vortex (b). Regions where particles have chaotic, irregular trajectories are the chaotic mixing regions, while regular trajectories are seen in the regions of invariant tori where the fluid is not mixed but only stirred. Outside the polar vortex (a), chaotic mixing region is recognized in midlatitudes. Closed loops of dashed line found at the both sides of the mixing zone are invariant tori. The one inside the mixing zone (blue, dashed line) coinsides with steep PV gradient at the polar vortex edge. One more torus of croissant shape is also found just outside of the edge (red line). Another chaotic mixing region is found inside the polar vortex (b) with more complicated structure of invariant tori; (1) central region of the polar vortex (green, solid loop), (2) three ``islands'' surrounding the central region, which are identified with three red loops, and (3) four thin islands just outside the three islands. These are transport barriers of different type from the polar vortex edge which are not related to any steep PV gradient.
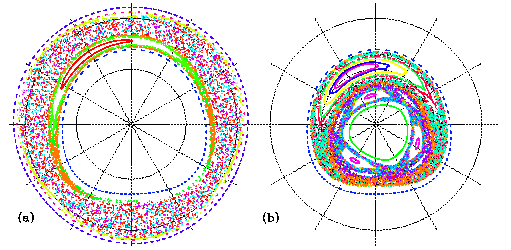
Fig.2 Poincare section for the quasi-periodic solution. Initial 12 points are located outside the vortex (a) and 19 points are inside (b).
We make circles with a radius of 0.05 rad centered on the points at which the finite-time Lyapunov exponent for Ä=2 days is highest inside and outside of the vortex, respectively. Initially we put 104 particles randomly in the circle and computed their trajectories for 90 days in order to have fundamental pictures of the mixing process.
Results for the aperiodic solution are shown in Fig.3. The particles outside the vortex (red) are well-mixed in 90 days. At first, particles are stretched out to west and east by the meridional shear of the jet. They become distributed on a thin line element surrounding the polar vortex. At the same time, the element is distorted and folded at several places. Such stretching and folding processes are repeated and the layered structures of the particles are made. Combined with the positive Lyapunov exponents, chaotic mixing dominates the large-scale mixing process. Transport barriers exist at the both boundaries of the chaotic mixing zone, just on the vortex edge that is defined as the largest meridional gradient of PV at each longitude. While planetary-wave breaking events make a small amount of the particles go outside of the vortex for 90 days, there are no incoming particles from outside during the period.
Particles inside the polar vortex are also mixed in a similar way (blue). But they do not spread all over the vortex inside. Several empty regions exist even at t=90 days; the core of the vortex, three small "island" regions surround the core region, and a croissant-shape region near the vortex edge. The method of Poincare section cannot be used for aperiodic solutions, but some features obtained in Fig.2 for the quasi-periodic solution have correspondence with empty regions found in Fig.3; isolation of the central region of the polar vortex, the croissant-shape region, and the three islands surrounding the central region.
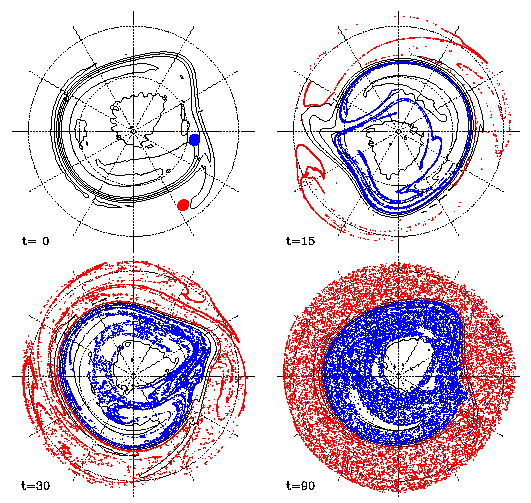
Fig.3 Advection of 10000 particles for 90 days in the aperiodic solution.