3-D Model simulations of $\rm SF_6$ with mesospheric chemistry

Thomas Reddmann, Roland Ruhnke and Wolfgang Kouker

FIGURES

Abstract

 

Multiannual integrations with the KArlsruhe SImulation model of the Middle Atmosphere (KASIMA) have been performed using meteorological analyses of vorticity and divergence up to 10 hPa to analyse the influence of a simplified $\rm SF_6$ mesospheric chemistry on estimation of mean age of air and to compare profiles of $\rm SF_6$ mixing ratios observed in the stratosphere with model simulations. The chemical degradation scheme includes electron attachment of $\rm SF_6$ and subsequent reactions of $\rm SF_6^-$, such as photodetachment and charge transfer with ozone. Several combinations of reaction rate constants and electron profiles have been tested. Good agreement with observations is found for inert $\rm SF_6$ transport. However, when mesospheric loss is included in the model significant deviations are found for polar winter observations above 25 km. Chemical loss by electron attachment without reactions yielding $\rm SF_6$ again is not compatible with observations. The atmospheric lifetime of $\rm SF_6$ spans 400 to 10000 years, depending on the assumed loss mechanism and the value for the electron density in the stratosphere.

 

Introduction

The chemically quasi-inert gas $\rm SF_6$ is widely used to characterize stratospheric transport, which is important to know for estimating the global burden of greenhouse gases or substances harmful to the ozone layer. As $\rm SF_6$ exhibits a quasi-linear and strong growth in its mixing ratio in the troposphere (Maiss and Levin, 1994) a mean age of stratospheric air can be deduced from the time lag since the troposphere last showed the mixing ratio measured in the stratosphere (see eg. Hall and Plumb, 1994; Harnisch et al., 1996; Hall and Waugh, 1998; Volk et al., 1997). Small deviations from linearity of the trend can be corrected in determining the mean age (Hall and Waugh, 1998; Volk et al., 1997). Generally, the derived maximum mean age of air in the stratosphere spans 4-5 years in the tropics up to about 10 years for polar winter observations. Recently, mesospheric loss of $\rm SF_6$ was discussed to explain obvious discrepancies between age determinations with $\rm SF_6$ versus other trace gases (Strunk et al., 2000; Harnisch et al., 1998) and discrepancies between circulation models and observations which consistently show lower age values than observed (Hall and Waugh, 1998). In their study Hall and Waugh used a range of constant loss rates above 60 km, which were compatible with the chemical lifetimes given in literature and showed that mesospheric loss, when unaccounted for, causes an overestimation of the mean age by up to 65 percent at subarctic latitudes and a height of 30 km. However, this effect strongly depends on the loss rates assumed.

In order to make more realistic comparisons with the observations, a simplified chemistry of $\rm SF_6$ is included in a 3-D model of the middle atmosphere based on meteorological analyses. The results are then compared with the $\rm SF_6$ profiles observed.

Chemistry of $\rm SF_6$ in the middle atmosphere

Mesospheric loss of $\rm SF_6$ has been evaluated by different authors: specific global lifetimes of 13 500 and 4200 years respectively were found when assuming either Lyman-$\alpha$ or a dissociative electron attachment to destroy the molecule (Ravishankara et al., 1993). When assuming photodissociation by UV radiation with a wavelength of less than 240 nm, a lifetime of 1000 years was estimated (Ko et al., 1993). In 2-D model calculations even an atmospheric lifetime as low as 800 years was found (Morris et al., 1995). For our study we use a simplified chemistry scheme (Reddmann et al., 2000), but besides electron attachment and photodissociation we also consider reactions of $hexafm$ and evaluate uncertainties of reaction rate constants by comparing several chemical scenarios.

The reaction of $\rm SF_6$ in the mesosphere can be described by the following scheme which extends that given by Odom et al. (1975) by adding the reactions of $\rm SF_6^-$:

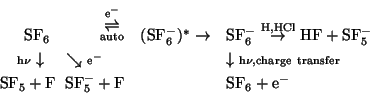
\begin{eqnarray*} \textstyle \rm SF_6 \hspace{10mm} \stackrel{e^-} {\stackre... ...yle \rm SF_5 + F \hspace{2mm} \rm SF_5^- + F & & \rm SF_6+ e^- \end{eqnarray*}



Reaction rates used are given in 1, note the variants for reaction R8. Details of the chemistry scheme are given in Reddmann et al. (2000).


Table 1: Reaction rates constants of reactions of $\rm SF_6$ and $\rm SF_6^-$ and expected rates for standard atmospheric conditions at 60 km, included in the chemical scheme.
Id Reaction Total rate constant in $10^{-9} \rm cm^{-3} s^{-1}$ or $s^{-1}$ Rate at 60 km in $\rm s^{-1}$ Remarks
R1 $\rm SF_6+ h\nu \to products$     destructive
R2 $\rm SF_6+ \rm e^- \to \rm (SF_6^-)^*$ 270 $1.2 \times 10^{-4}$  
R2a $\rm SF_6+ \rm e^- \to SF_5^+ + F, ...$     destructive branch of R2, branching fraction $< 0.001 $
R5 $\rm (SF_6^-)^*+ M \to \rm SF_6^-$ 0.19    
R6 $\rm (SF_6^-)^*\to \rm SF_6+ e^-$ $ 1 \times 10^{-6}$    
R3 $\rm SF_6^-+ \rm h \nu \to \rm SF_6+ e^- $   0.3 Photodetachment
R4 $\rm SF_6^-+ H \to SF_5^+ + HF$ 0.21 $1.2 \times 10^{-4}$ destructive
R7 $\rm SF_6^-+ \rm HCl \to products$ 1.5 $0.02$ destructive
R8a $\rm SF_6^-+ \rm O_3 \to \rm SF_6+ O_3^-$ 0.032 $0.18$  
R8b $\rm SF_6^-+ \rm O_3 \to \rm SF_6+ O_3^-$ 1.2 $6.8$  


Figure 1: Electron density profiles used in model runs, midlatitude winter conditions at noon, see text for description of versions.
\includegraphics*[width=85mm, trim=0 0 0 0]{jgr9904.eps}

The result of the chemistry scheme of $\rm SF_6$ depends on the assumptions made for some reaction rates and electron density. To test the influence of various parameters we choose several combinations in the model runs. The electron density profile is represented by four versions to account for the uncertainties especially in the mean electron energy and to test the influence of diurnal and seasonal variation, see Fig. 1. All scenarios tested are given in Table 2.


Table 2: Different scenarios of $\rm SF_6$ chemistry in model runs
Notation Description Electron profile
S1 direct loss by electron attachment (R2) B
S2 S1 + R3 + R4 + R5 B
S3 S2 + R7 + R8a B
S4 as S3, but R8b B
S5 as S3 B1
S6 as S3 + R6 B
S7 as S4 A
S8 as S7 + cosmic ray ionisation A1
See text for versions of electron profiles,
see Table 1 for the identification of reactions.

 

Model description and experiments

Model experiments have been performed with the KASIMA model, see Kouker et al. (1999). For the present studies, an updated model version was applied allowing for a vertical resolution that is variable with height. The model extends from 10 km to 120 km with 63 layers. From the lower boundary up to 25 km, the vertical resolution is 750 m. From 25 km up to the upper boundary the vertical spacing between the levels gradually reaches 3.8 km. The triangular truncation T21 corresponds to a horizontal resolution of about $5.6^o \times \ 5.6^o$. At the lower boundary, the geopotential and temperature fields are given by the analyses of the European Centre of Medium range Weather Forecast (ECMWF) and the model is relaxed to the analyzed temperature, divergence and vorticity using a forcing term with a time scale of 4 h below 10 hPa. Above 10 mb, the primitive equations are integrated without additional forcing.

The trend of $\rm SF_6$ is described by the function of Volk et al. (1997) (their equation (15)) and their expression for the mean age is used. The $\rm SF_6$ mixing ratio is set according to the trend function within an equatorial $\pm 15 \deg$ wide belt extending up to 100 hPa, thus simulating the intrusion into the tropical pipe (Plumb, 1996). As a rough initialization a linear profile between 15 and 35 km ranging from 0 to 7 years is assumed.

At first, the model has been run for 5 years using repetitive ECMWF analyses of the year 1990 to establish stationary conditions. After that, the model was run using the ECMWF analyses of the years 1990 - 1997. Hence, the model results include the appropriate meteorological conditions for comparison with observations of different authors (Harnisch et al., 1996; Strunk et al., 2000; Patra et al., 1997; Moore, 1999). All eight scenarios for $\rm SF_6$ chemistry were run with the model and in addition a pure inert tracer was transported.

 

Model results of mean age and comparison with observations

Inert tracer

Figure 2: Zonal mean of mean age for December, March, June, and September averages for the years 1990 - 1998 (inert tracer)
\includegraphics*[trim=0 0 0 0]{jgr9907.eps}

Figure 3: Time-height cross section of mean age at the equator for 1990 - mid 1998
\includegraphics*[trim=0 0 0 0]{jgr9908.eps}

To give a general impression of the characteristics of the model transport, Figure 2 shows the zonal mean age for the months of December, March, June and September, averaged over the years of 1990 - 1998 for the inert tracer. The figure shows the typical features observed for inert tracers: for a specific height level the younger mean age values are found near the equator, such showing the mean ascent within the tropical pipe; at high latitudes, the season strongly affects the mean age distribution by ascent above the summer pole and descent above the winter pole. The mean age values are in the range of other model studies (Waugh et al., 1997, see e.g.). Figure 3 gives a time-height cross-section at the equator of mean age. The 2-year's isochrone clearly shows the effect of the QBO as an oscillation of mean age with an approximate period of 2 years. In addition, the upwelling expected during the QBO phase when the equatorial zonal winds at 30-50 hPa are easterly (Gray, 2000), e.g. spring 1992, is reflected by younger mean age values at 30 hPa.

In Figure 4 mean age observations are compared with the pure inert tracer profiles of the mean age of the model. The exact locations as well as the exact time of the balloon observations during the flights may deviate from the nominal values and errors may have been introduced in the comparisons. Therefore, the corresponding model results are shown for nine gridpoints (longitude, latitude) lying absolutely nearest to the observations. This also gives some indication of the variation within the model. If original mixing ratio data were available, mean age was reevaluated from these data using the same function as in the model. The correction for age spectral width yields somewhat higher age values than those given by Harnisch et al. (1996).

Figure 4: Observed and modelled age profiles of the inert tracer for different dates and locations (see text for references). The model profiles are taken at nine gridpoints nearest to the location of the observation.
\includegraphics*[trim=0 0 0 0]{jgr9911.eps}

Figure 5: Observed and modelled age profiles for different dates and locations (see text for references) and different chemistry scenarios. The model profiles are interpolated to the location of the observation.
\includegraphics*[scale=0.8, trim=0 0 0 0]{jgr9912.eps}

The main properties found can be summarized as follows: In general, we find a satisfactory agreement between the observations and model results of the inert tracer. Some polar model profiles have the tendency to show higher age values than the observations above about 25 km, especially in the year 1997. The sharp onset of a plateau in the age values evident in the observations often seems to be smeared out or shifted in height for the model. Exceptionally, profile P9 shows a constant shift to higher values observed over all altitude levels. The profiles observed in northern late spring 1997 show a rather high variation of the data (P14, P15). Here, also $\rm CO_2$ measurements exist. Both tracer observations are consistent with the assumption of highly filamentary air masses of different origin (polar vortex - midlatitudes). This conclusion is supported by the fact that our model profiles show a break in the vertical profile (P14) or crossing profiles in the environment (P15). In-situ measurements are expected to randomly detect even very small spatial inhomogeneities. However, the model resolution is about 500 km in both horizontal dimensions, so differences are expected in such cases. The very low age values of the tropical profile P5 are not reproduced in the model, whereas the situation of March-92 (profile P3, at $20^o$E, $68^o$N), where the observations show younger airmasses above older ones, shows up to some extent in the model.

 

Tracers with chemistry

The effects of $\rm SF_6$ chemistry are shown in Figure 5. In the following sections, the expression of effective mean age shall be used for age values derived when chemical loss is included. Scenario S8 has been left out in the figure, as the difference between S7 and S8 is typically smaller than 0.2 y up to 30 km. This value is only exceeded in the polar night where chemical tracers show much higher differences to the observations. The modelled profiles of the different chemistry scenarios are interpolated to the location of observation. Consequently, the information about the neighbourhood is not shown in this plot. Generally, the chemical loss is supposed to be most pronounced for polar winter profiles after the descent of air masses in the polar vortex region, which is clearly seen in Figure 5 for profiles taken in polar winter/spring. But even for tropical profiles, chemical loss is observed for scenario S1. For the comparison with the model tracers including $\rm SF_6$ chemistry, only some profiles are selected. The tropical profile P12 shows very good agreement with the observation up to 25 km. Above, the model shows an effective mean age up to one year higher than observed for all chemistry scenarios. For scenario S1, however, the effective mean age is 2.5 years too high. In this scenario a purely destructive attachment reaction is assumed. As no $\rm SF_6$-stabilizing reaction is included, this chemistry scenario gives the maximum $\rm SF_6$ loss for a given electron profile. This large difference shows that the possibility of an attachment reaction without reactions reforming $\rm SF_6$ can be excluded. For the chemistry scenario S3, also a strong loss is expected, as only the destructive reaction with $\rm HCl$ and the weak version of the charge exchange reaction with $\rm O_3$ are included. This can be seen in the profiles P6 above 25 km and P15 at 27.5 km. Both observations are taken at midlatitudes and exhibit an undisturbed profile above 23 km. Here, S3 and S5 significantly deviate from the observations, but the inert profile and the more stable chemistry profiles are still compatible.

 

Discussion

Comparing the different scenarios used in the model runs, the inert tracer gives the best agreement with the observations. This is surprising, as several studies favour mesospheric loss to explain inconsistencies between different tracers (Strunk et al., 2000; Harnisch et al., 1998) or models (Hall and Waugh, 1998). The transport properties of the present KASIMA version seem to be not untypical for 3D models of the stratosphere. For example, the mean age distributions shown in Figure 2 compare well with the distributions shown by Waugh et al. (1997). Somewhat higher mean age values in the upper stratosphere may be explained by the higher upper boundary of the present model. A satisfactory agreement of the model is found for the latitudinal profiles of mean age at about 20 km derived from aircraft obserations made in the months of October/November (Waugh et al., 1997, Fig. 10). The mean age values also compare well with simulations made using isentropic models (A. Iwi, personal communication). On the other hand, our model yields generally higher mean age values than those models presented in the study of Hall et al. (1999) . Harnisch et al. (1999) derived mean age values from $\rm CF_4$ measurements of about 10 years at about 60 km height and about 7 years at about 30 - 40 km. This compound is believed to show a negligible loss even in the mesosphere. The stratospheric values are in accordance with our model, but the high mesospheric values are not reached in the model. Consequently, our simulation seems to yield too young an age for that height.

The observed $\rm SF_6$ age profiles shown in Fig 4 are characterized by a rapid increase of age up to a certain height. Here, we find a convincing agreement between the observations and the model up to about 22 km for most profiles, irrespective of the latitude and season. This may be compared with the study of Hall et al. (1999)(their Figure 5), in which most models a far too young compared to the observations. Above that height, a plateau in the age value is often indicated in the observations. Whereas this plateau seems to be smoothed in the simulations, the altitude level and the value of the plateau are reproduced for most tropical and midlatitude profiles. In the case of profile P5, it is difficult to explain the mean age observations of only 2.5 years at 35 km height by common transport processes. Furthermore, profile P9 is exceptional in its high age values for the whole altitude range. We therefore conclude that in cases where mesospheric loss is not expected to influence the profiles, the agreement between the model with an inert tracer and observations is satisfactory.

In the case of high latitude observations, the picture is quite different. As already mentioned, even the simulations for the inert tracer at and above 25 km, especially in 1997, give consistently higher age values than those observed. As the chemical effect would only lead to apparently older air masses, the reason for these discrepancies must lie in the transport properties of the model. Deficits of the model's overall meridional circulation or incorrect match of polar vortex air and midlatitude air masses in the comparisons, especially near the vortex edge, may cause these deviations. The variation of the profiles in the proximity of the observation, shown in Figure 4 for profiles P10, P11, and P13, would support the latter suggestion. For all polar winter profiles at maximum height levels, the inert tracer gives the best agreement, chemistry scenarios S3 and S5 are very difficult to reconcile with the observations.


Table 3: Deduced atmospheric lifetime of $\rm SF_6$ for the different chemistry scenarios, see Table 2
Notation Lifetime in years
S1 472
S2 6232
S3 1830
S4 6360
S5 2597
S6 9379
S7 4550
S8 614


Using loss rates and the corresponding mixing ratios in the model, atmospheric lifetime can be deduced for the different chemistry scenarios. As $\rm SF_6$ exhibits a strong trend, only the so-called instantaneous lifetime $\tau(t)$ can be given:


\begin{displaymath} \langle \tau (t) \rangle = \langle \frac{\int n dV}{\int \lambda ndV} \rangle \end{displaymath} (1)

where $n$ is the local number density of the trace gas and $\lambda$ denotes the local loss frequency. The brackets mean annual average. The result is given in Table 3 as a mean for the years 1990 - 1998. A range of mean atmospheric lifetimes between 400 and 10000 years is deduced, with the expected trend of long lifetime for chemistry scenarios including all stabilizing mechanisms. The lower value found for scenario S1 is of the order of the value given by Morris et al. (1995) who find a lifetime of 800 years. Harnisch et al. (1999) conclude from their analysis, that $\rm SF_6$ must have a much higher atmospheric lifetime of about 5000 years; thus our findings support their conclusion. For the atmospheric lifetimes a strong semiannual oscillation (for example a 25% amplitude for scenario S4) was found, but no significant trend or other periodicity.

The low lifetime for scenario S8 compared with scenario S7 can be explained by the non negligable chemical loss in the stratosphere caused by cosmic ray ionisation. Obviously, stratospheric loss strongly influences atmospheric lifetime, but for profiles of mean age, the effect of stratospheric loss is small.

 

Conclusions

Mesospheric loss of $\rm SF_6$ could not be identified uniqueley in the observations made so far in comparison with our simplified chemistry scheme. Our findings contradict $\rm SF_6$ loss without a stabilization process. The comparisons with the model simulations favor a longer lifetime of $\rm SF_6$ in the middle atmosphere, which is caused by charge exchange reactions of $\rm SF_6^-$ and its photodetachment.

The atmospheric lifetimes found for the different chemistry scenarios differ by more than an order of magnitude. Stratospheric loss may be important for $\rm SF_6$ lifetime, without considerably affecting the $\rm SF_6$ profiles. Therefore, in order to estimate the possible contribution of $\rm SF_6$ to global warming, studies with a more detailed stratopsheric ion chemistry, including the energy spectrum of free electrons are necessary.

The transport properties of 3D models are also an important parameter when studying chemical loss of $\rm SF_6$. Correlation studies with other quasi-inert tracers, such as $\rm N_2O$, $\rm CO_2$ and $\rm HF$ would allow to separate more clearly the dynamically and chemically caused transformations of the $\rm SF_6$ mixing ratios. In addition, a higher horizontal resolution seems to be necessary to reproduce the observations taken near the vortex boundary or in highly inhomogeneous air masses, as found in June 1997 in midlatitudes.

On the other hand, winter/spring polar $\rm SF_6$ profiles taken inside the polar vortex at heights above 35 km should definitely show mesospheric loss effects. Unfortunately, accurate in-situ observations of $\rm SF_6$ in this region of the stratosphere have only been sparse and often have been taken near the vortex boundary. Therefore observations at higher altitude in the polar night are highly desirable to confirm chemical loss effects of $\rm SF_6$ and to specify the reactions involved.

We would like to thank I. Langbein for preparing the ECMWF data, A. Engel and M. Strunk for providing their data prior publication, J. Harnisch for sending us the $\rm SF_6$ data in electronic form, and B. Fichtelmann for providing UV solar flux data. We also thank ECMWF for permitting us to use their data and the DKRZ in Hamburg for their kind assistance. U. Schurath gave helpful comments during the preparation of the manuscript. The very detailed report of an anonymous referee is highly appreciated.

 

References

Gray, L. J., A model study of the influence of the quasi-biennial oscillation on trace gas distributions in the middle and upper stratosphere, J. Geophys. Research, 105, 4539 - 4551, 2000.

Hall, T. M., and R. A. Plumb, Age as a diagnostic of stratospheric transport, J. Geophys. Research, 99, 1059-1070, 1994.

Hall, T. M., and D. W. Waugh, The influence of nonlocal chemistry on tracer distributions: Infering of mean age from $\rm SF_6$, J. Geophys. Research, 103, 13327 - 13336, 1998.

Hall, T. M., D. W. Waugh, K. A. Boering, and R. Plumb, Evaluation of transport in stratospheric models, J. Geophys. Research, 104, 18815 - 18838, 1999.

Harnisch, J., R. Borchers, P. Fabian, and M. Maiss, Tropospheric trends for $\rm CF_4$ and $\rm C_2F_6$ since 1982 derived from $\rm SF_6$ dated stratospheric air, Geophys. Res. Lett., 23(1), 1099-1102, 1996.

Harnisch, J., W. Bischof, R. Borchers, P. Fabian, and M. Maiss, A stratospheric excess of $\rm CO_2$ - due to tropical deep convection?, Geophys. Res. Lett., 25(1), 63-66, 1998.

Harnisch, J., R. Borchers, P. Fabian, and M. Maiss, $\rm CF_4$ and the age of mesospheric and polar vortex air, Geophys. Res. Lett., 26, 295 - 298, 1999.

Ko, M. K., N. D. Sze, W.-C. Wang, G. Shia, A. Goldman, F. J. Murcray, D. G. Murcray, and C. P. Rinsland, Atmospheric sulfur hexafluoride: Sources, sinks and greenhouse warming, J. Geophys. Research, 98, 10499 - 10507, 1993.

Kouker, W., I. Langbein, T. Reddmann, and R. Ruhnke, The Karlsruhe simulation model of the middle atmosphere version 2, Wissenschaftliche Berichte des Forschungszentrums Karlsruhe, FZKA 6278, 1999.

Maiss, M., and I. Levin, Global increase of $\rm SF_6$ observed in the atmosphere, Geophys. Res. Lett., 21, 569 - 572, 1994.

Moore, F. e., First in situ gas chromatograph on a balloon platform yielding tracer measurements with improved spatial resolution, J. Geophys. Research, to be submitted, 1999.

Morris, R. A., T. M. Miller, A. Viggiano, and J. F. Paulson, Effects of electron and ion reactions on atmospheric lifetimes of fully fluorinated compounds, J. Geophys. Research, 100, 1287 - 1294, 1995.

Odom, R. W., D. L. Smith, and J. H. Futrell, A study of electron attachment to $\rm SF_6$ and auto-detachment and stabilization of $\rm SF_6^{-}$, Journ. of Physics, B, 8, 1349 - 1366, 1975.

Patra, P. K., S. Lal, B. Subbaraya, C. H. Jackman, and P. Rajaratnam, Observed vertical profile of sulphur hexfluoride $\rm SF_6$ and its atmospheric application, J. Geophys. Research, 102, 8855 - 8859, 1997.

Plumb, R. A., A tropical pipe model of stratospheric transport, J. Geophys. Research, 101, 3957 - 3972, 1996.

Ravishankara, A., S. Solomon, A. Turniseed, and R. Warren, Atmospheric lifetimes of long-lived halogenated species, Science, 259, 194 - 199, 1993.

Reddmann, T., R. Ruhnke, and W. Kouker, 3-D model simulations of $\rm SF_6$ with mesospheric chemistry, J. Geophys. Research, p. submitted, 2000.

Strunk, M., A. Engel, U. Schmidt, C. M. Volk, T. Wetter, I. Levin, and H. Glatzel-Mattheier, $\rm CO_2$ and $\rm SF_6$ as stratospheric age tracers: consistency and the effect of mesospheric $\rm SF_6$-loss, Geophys. Res. Lett., 27, 341 - 345, 2000.

Volk, C., J. Elkins, D. Fahey, G. Dutton, J. Gilligan, M. Loewenstein, J. Podolske, K. Chan, and M. Gunson, Evaluation of source gas lifetimes from stratospheric observations, J. Geophys. Research, 102, 25543 - 25564, 1997.

Waugh, D., et al., Three-dimensional simulations of long-lived tracers using winds from MACCM2, J. Geophys. Research, 102, 21493 - 21513, 1997.

World Meteorological Organization (WMO), Scientific assessment of ozone depletion: 1998, Global Ozone Research and Monitoring Project, Rep. No. 44, 1999.

Back to

Session 1 : Stratospheric Processes and their Role in Climate Session 2 : Stratospheric Indicators of Climate Change
Session 3 : Modelling and Diagnosis of Stratospheric Effects on Climate Session 4 : UV Observations and Modelling
AuthorData
Home Page