Planet Ejection from Binary Systems
You can download the paper published on this research here in PDF format.
Summary
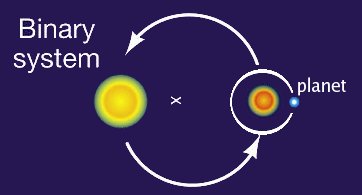Along with Yanqin Wu, I have also studied the orbital evolution of planets in binary systems.
Numerical studies have shown that such planets are prone to ejection from the system unless their orbits remain close enough to one of the two
stars (within about 1/10 of the orbital radius of the two stars). We analyically investigated the behavior of a planet orbiting a star (the "parent"
star) which has another "companion" star which orbits both the parent star and the planet. This setup is shown in the image to the right.
This sort of investigation can be thought of as a first step in determining how and where it's possible to form such a planet in the first place within such binary systems. Our main objective was to determine the physical reason/mechanism responsible for ejecting the planet.
We postulated that the planet ejection was due to resonance overlap. Resonance overlap has been shown to lead to chaotic diffusion of orbital parameters ("jerky" variations in eccentricity, orbital radius, etc). This chaotic diffusion can eventually lead the planet into a star-crossing orbit whereby it will suffer a close encounter and be ejected from the system. Despite this conjecture, our initial investigation showed that the overlap of mean-motion resonances was not extended enough to give the same results as the numerical experiments. We did find, however, that the overlap of mean-motion subresonances was able to reproduce the numerical results. These subresonances are not normally dynamically significant as they are degenerate and lie atop each other. However, the presence of the second star lifts the degeneracy as it causes the subresonances to shift apart from one another, thus producing larger regions of overlap.
The image shows a comparison between the results from numerical simulations and the results predicted by our analytical theory.
The white triangular area at the bottom of the graph shows stable regions, that is, parameter values of the planet's orbit for which it is
not prone to ejection from the system. The upper gray region, filled with dots, represents our predictions of parameter values for which the planet
would be unstable and thereby ejected from the system. The connected line of points is the dividing line between instability and stability as
predicted by numerical simulations. While the match does not look very close for all values, the numerical simulations were done over a very coarse
grid. The inset on the graph shows a zoom-in of part of the graph where we re-did the numerical experiments with a much finer grid. The small dots
are the same as on the main graph, but the new divsion between stability and instability based on the numerical simulations is now shown by the division
between the black squares and the dashes. This compares much better with our analyical results. The fingers of instability which stretch from right
to left are due to overlap of subresonances belonging to specific mean-motion resonances. Centroid positions of the latter have been labeled by the
orbital ratio of the resonance. The triangles on the main graph roughly trace the dividing line between stability and instability which our analytical theory predicts
based on overlap of mean-motion resonances, alone.