• Introduction
• Trends in temperatures and planetary wave propagation
• Brewer Dobson circulation
• Conclusions
• References

FIGURES

• Figure 1
• Figure 2
• Figure 3
• Figure 4
• Figure 5
• Figure 6
• Figure 7

Introduction

In this paper results from the troposphere-stratosphere configuration of the Met. Office Unified Model (UM) (Cullen 1993; Butchart & Austin 1998) are used to investigate changes in the stratospheric climate and Brewer-Dobson circulation due increasing Greenhouse Gas (GHG) concentrations. The model had a latitude-longitude resolution of 2.5 by 3.75 and 49 levels extending from the surface to 0.1 hPa ( km). It contained a comprehensive set of physical parameterizations for sub-grid scale processes. Orographic gravity wave drag was represented (Gregory et al. 1998) only up to 20 hPa and above that replaced by Rayleigh friction, though the drag coefficient was negligible between 20 and 1 hPa [see dashed curve in Fig. 1 of Butchart & Austin (1998)]. Also the longwave radiative cooling included the effects of the minor GHGs--CH, NO, CFC11, and CFC12, as well as CO.

Starting from conditions representative of the early 1990s the model was integrated for the 60 years 1992-2051 (run ``A'') assuming the Intergovernmental Panel on Climate Change IS92a scenario for GHG concentrations, but no changes in stratospheric ozone or water vapor (Butchart et al. 2000). Sea surface conditions were taken from a separate coupled ocean-atmosphere experiment using the same GHG scenario (Mitchell et al. 1995). The integration was repeated (run ``B'') using different initial conditions, but also from the early 1990s, and the two integrations were used by Butchart et al. (2000) to separate chaotic variability from the underlying trend.

Trends in temperatures and planetary wave propagation

Both runs predict a systematic global cooling of the stratosphere, which increases with height and is broadly consistent with past observed trends, though in the upper stratosphere the past trends are slightly larger. In polar regions trends were unpredictable. This was due to internal decadal variability resulting from unpredictable decadal variations in the Rossby wave flux from the troposphere which, nonetheless, systematically increased over the 60 years in both runs [See Figs. 1 and 2 which are taken from Butchart et al. (2000)].

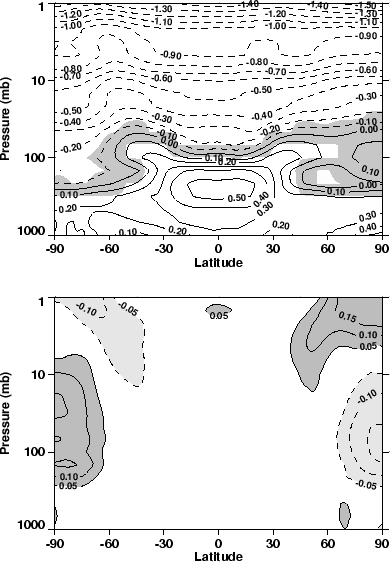
Fig. 1. Trends (K/decade) in the zonally averaged annual mean temperatures over the 60 years of run A. Shading indicates were the trends are not significant at the 95% confidence level. The lower panel shows the trend in run B minus the trend in run A and indicates the unreliability of quantitative predictions of temperature trends in the high latitudes in this model.

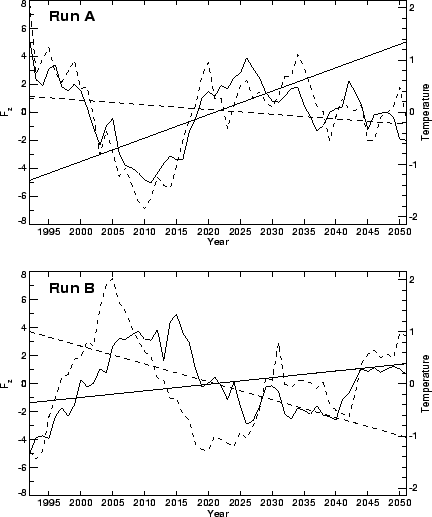
Fig. 2. Comparison between 10 hPa temperatures and the vertical component of the EP flux () at 100 hPa for the northern winter (DJF). The curves are deviations from the 60 year mean with the linear trend (the straight lines) removed and further smoothed by an 11-year running mean. Dashed lines are the temperatures (K) averaged poleward of 60N and the solid lines ( Kg s) averaged poleward of 40N. Similar conclusions can be inferred from the results for the southern winter.

The systematic increase over the 60 years in seen in Fig. 2 is part of a more general increase in the flux of wave activity from the troposphere which occurs in every seasons and in both hemispheres (see Fig. 3). The largest changes tend to be in the lower to middle latidues. Despite the increase in the amplitude of the EP flux vectors the model results show little evidence of any significant change in the wave focusing (i.e. the direction of the flux vectors) in the sub-tropical lower stratosphere, as has been found in the analysis of ``doubled CO'' experiments (Rind et al. 1998).

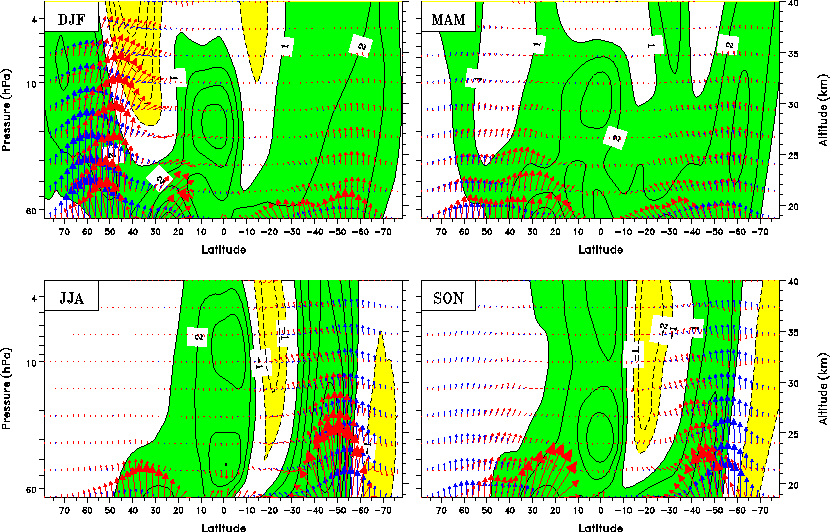
Fig. 3. Seasonal mean EP flux at the start of run B (blue arrows) and the change () over the 60 years (red arrows). The flux vectors have been multiplied by the cosine of latitude to give the natural form for plotting in the latitude-height plane (Dunkerton et al. 1981) and have been further scaled such that the distance occupied by 10 of latitude represents a value of Kgs and that occupied by 10 km in altitude represents a value of Kgs. Also shown is the change in the zonal mean zonal wind in ms. Green shading denotes a westerly shift and, yellow, an easterly shift. Results shown here were taken from a least squares linear fit to the yearly data. A broadly similar picture is given by the results of run A.

Brewer Dobson circulation

The Brewer-Dobson circulation is a global-scale cell in the stratosphere in which air rises in the tropics and then moves polewards and downwards, mostly in the winter hemisphere Because it describes Lagrangian-mean. transport it can not be diagnosed directly from the UM integrations. Instead we have calculated the transformed Eulerian mean residual velocities ( , ) (Andrews & McIntyre 1976; 1978) which approximate the mean meridional mass transport for seasonally averaged conditions (e.g., Holton 1990). Averaged over the 60 years the residual velocities indicate the model is able to correctly reproduce the classical Brewer-Dobson picture of a meridional overturning circulation (see Fig. 4). In agreement with observations the maximum upwelling occurs in the summer hemisphere.

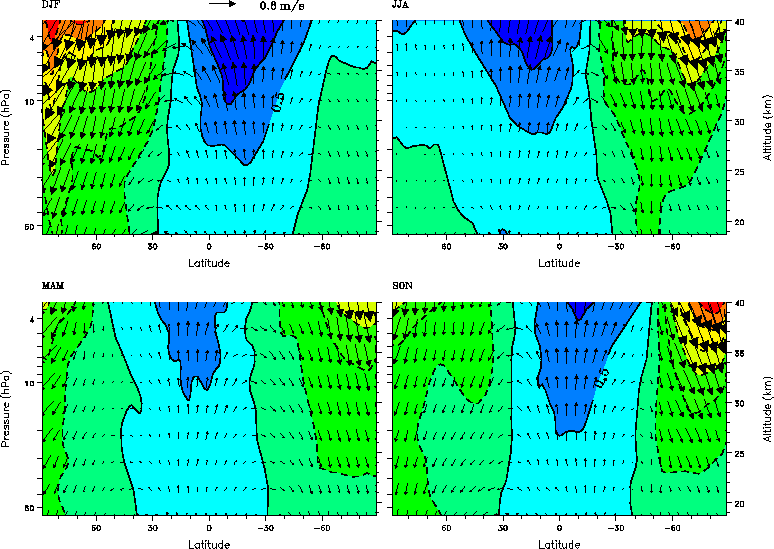
Fig. 4. Sixty year mean residual velocities ( ) for each season of run B (run A results are very similar). The contours show the strength, in mms, of the vertical component, , with dashed contours indicating descent and blue shading ascent.

In each model year the smallest upward mass flux entering the lower stratosphere was in June-August (JJA) and the largest in December-February (DJF)(Fig. 5), presumably because of the stronger extra-tropical wave-driving in the northern winter. In the ``1990s'' the modeled mass fluxes are in broad agreement with mass fluxes derived from observations (Rosenlof 1995). At the same time, the mean vertical velocity from 12N to 12S (not shown), varied from mms in JJA to mms in DJF, slightly less than the 0.2-0.4 mms inferred from the so-called ``tape recorder'' signal seen in water vapor measurements (Mote et al. 1995). The tape recorder signal is a manifestation of the annual cycle in the tropical lower-stratospheric temperatures resulting from the annual cycle in the upwelling (Yulaeva et al. 1994). Our simulated annual cycle in tropical lower stratospheric temperatures (see Fig. 6, for run B) had the correct amplitude and, notably, the amplitude did not change significantly over the 60 years, despite the predicted cooling of the lower stratosphere. Consistently, the trends in the tropical upwelling were roughly the same in every season (Fig. 5) with the combined effect of a 18% (19% for run A) increase in the annual mean upwelling by 2051.

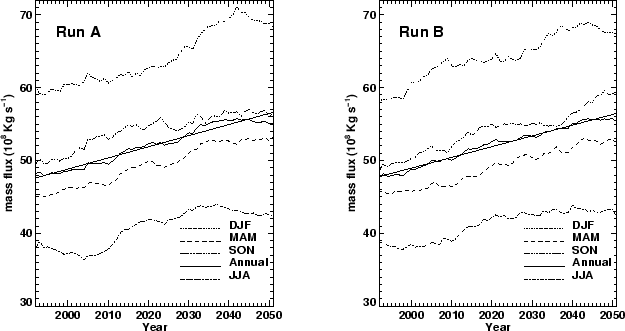
Fig. 5. Seasonal and annually averaged upward mass fluxes at 68 hPa. The curves are 11 year running means and the straight lines are least squares fits to the annual mean results.

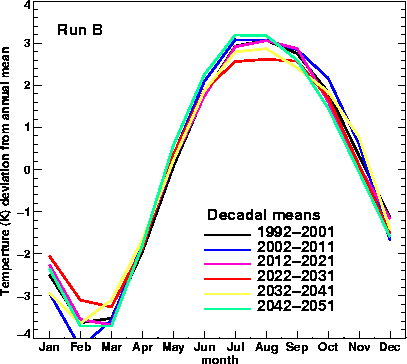
Fig. 6. The trend in the mass flux is fairly uniform throughout the year as indicated by the absence of any change in the decadal mean amplitude of the annual cycle in the mean temperatures from 20N-20S at 68 hPa.

The main reason for this increase in upwelling was increased extra-tropical planetary wave driving. For steady seasonal mean conditions the Cambridge ``downward control'' principle (Haynes et al. 1991) gives the vertical mass flux poleward of latitude at height , in terms of the vertical integral of the zonal forces, , above; or more specifically

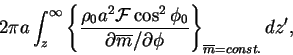
where is the earth's radius and a basic state density. The integration is up a line of constant zonal mean absolute angular momentum (Haynes et al. 1991). At the latitudes used in our calculations these surfaces were nearly vertical, hence we used, instead, constant latitude. For the model, is the sum of the resolved planetary wave forcing given by the Eliassen-Palm (EP) flux divergence, numerical dissipation and unresolved forcing represented by the parameterized orographic gravity wave drag up to 20 hPa and Rayleigh friction above that. The latter was, however, negligible below 1 hPa and, because of the density weighting of the integrand, had only a small effect on the mass fluxes in the lower stratosphere.

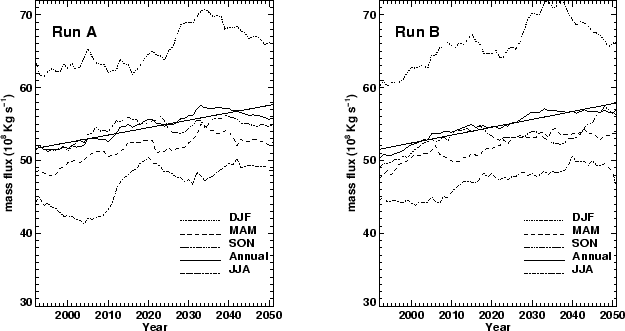
Fig. 7. Seasonal and annually averaged extra-tropical downward mass fluxes at 68 hPa derived from the planetary wave driving by the Cambridge downward control principle. The curves are 11 year running means and the straight lines are least squares fits to the annual mean results.

Quantitatively the mass fluxes derived from the EP flux divergence agreed well in every season with those obtained directly from the residual vertical velocities (cf. Figs. 5 and 7). The downward control mass fluxes were slightly larger, partly because of the absence of a small negative contribution from the Rayleigh friction--in the mesosphere zonal mean zonal winds at the turnaround latitudes (i.e. where the vertical velocities change direction) were generally easterly--and also probably because of the missing contribution from orographic gravity wave drag which was not archived from our runs. However, the dominant contribution to the extra-tropical downward flux at 68 hPa came from the EP flux divergence and, in every season, increased over the 60 years (Fig. 7). Furthermore, the 60 year increase of Kgs in the wave-driven annual mean downward mass flux in run B, for example, balances most of the Kgs increase in the tropical upwelling, confirming that the strengthening of the Brewer-Dobson circulation was predominantly wave driven in the model.

The increased wave driving strengthening the Brewer-Dobson circulation is most likely a direct consequence of more wave activity emanating from the trosposphere in the region of the trunaround latitudes where the residual vertical velocities change direction (Fig. 3). In contrast to the analysis of ```doubled CO'' (Rind et al. 1998), contributions to increased wave-driving from changes in the focussing of the waves was small because of the absence of any significan change in the direction of the EP flux vector (again see Fig.  3)

Conclusions

• The model predicts an overall cooling of the stratosphere which increases with height.
• In the polar stratosphere quantitative temperature trends are unpredictable due to unpredictable decadal variability in the planetary wave driving from the troposphere.
• The model predicts an increase in the flux of planetary wave activity emanating from the troposphere, especially in the sub-tropics.
• No significant change is predicted in the direction of the EP flux in the sub-tropical lower stratosphere.
• The model correctly reproduces the Brewer-Dobson circulation with the mass fluxes between the stratosphere and troposphere broadly in agreement with observational estimates.
• The mass exchange rate between the stratosphere-troposphere is predicted to increase by 3% per decade.
• The increases in the mass exchange rate occur in all seasons (e.g. there is no change in the amplitude of the annual cycle in the tropical tropopause temperatures.
• By downward control the increased mass fluxes can be accounted for by the increased planetary wave-driving resulting from extra wave activity emanating from the troposphere.
• Change in the direction of wave propagation do not appear to be significant factor in the stratosphere.
• The increases in the mass exchange rate between the troposphere-stratosphere are of particular relevance to ozone and climate prediction because of the effects on the removal of chlorofluorocarbons (CFCs) and other GHGs from the atmosphere (Butchart & Scaife 2000).

References

Andrews, D. G., M. E. McIntrye, J. Atmos. Sci. 33, 2031 (1976).

---, ---, J. Atmos. Sci. 35, 175 (1978).

Butchart, N., J. Austin, J. Atmos. Sci. 55, 2782 (1998).

---, ---, J. R. Knight, A. A. Scaife, M. L. Gallani, J. Climate 13, 2242 (2000).

---., A. A. Scaife, submitted to Nature.

Cullen, M. J. P., Meteor. Mag. 122, 81 (1993).

Dunkerton, T., C.-P. F. Hsu, M. E. McIntyre, J. Atmos. Sci. 38, 819 (1981).

Gregory, D., G. J. Shutts, J. R. Mitchell, Quart. J. Roy. Meteor. Soc. 124, 463 (1998).

Haynes, P. H., C. J. Marks, M. E. McIntyre, T. G. Shepherd, K. P. Shine, J. Atmos. Sci. 48, 651 (1991).

Holton, J. R., J. Atmos. Sci. 47, 392 (1990).

Mitchell, J. F. B., T. C. Johns, J. M. Gregory, S. F. B. Tett, Nature 376, 501 (1995).

Mote P. W., et al., J. Geophys. Res. 101, 3989 (1996).

Rind, D., D. Shindell, P. Lonegan, N. K. Balachandran, J. Climate 11, 876 (1998).

Rosenlof, K. H., J. Geophys. Res. 100, 5173 (1995).

Yulaeva, E., J. R. Holton, J. M. Wallace, J. Atmos. Sci. 51, 169 (1994).