Previous: Effective diffusivity Next: Conclusions Up: Ext.

6. Geometric properties

We next consider how certain recent ideas from the theory of dynamical systems may be applied to the observed velocity fields in the region of the tropopause. We focus on the location of certain geometric structures, in particular the invariant (stable and unstable) manifolds and uniform hyperbolic trajectories. Recent extensions of the theory of time periodic flows to aperiodic flows, as well as new methods and algorithms for extracting the geometric structures can be found in Malhorota & Wiggins (1998), Haller (2000), Lapeyre et al. (2000), where the reader is also directed for further details and definitions. Recent applications of some of these and other ideas to problems of mixing in geophysical flows can be foud in, eg., Haller & Poje (1998), Bowman (2000), Binson & Legras (2000).

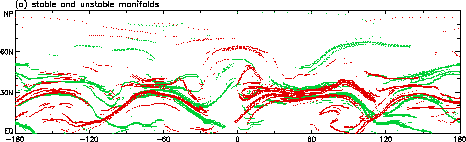
Figure 4a shows the stable and unstable manifolds calculated by the finite strain method described in Bowman (2000) and Joseph & Legras (2000), which involves advecting a grid of particles and a pertrubed grid for a finite time both forwards and backwards in time and noting the pairs of initial conditions that reach a given separation (here 50 time the initial separation). The green shading in the figure represents those particles that separate forward in time (mapped back to their initial locations), thus representing the global stable manifolds. Similarly the red shading represents the global unstable manifolds. Consideration of the PV field at this time, Figure 4b, shows the manifolds to align predominantly along the equatorward flank of the high PV gradients of the tropopause. Further, suggestions of local hyperbolic regions, indicated by the transverse intersections of the stable and unstable manifolds can be seen equatorward of Rossby wave undulations reaching breaking amplitudes.

In an attempt to refine the local picture of manifold intersections, we implemented the Jacobain method of Haller (2000) for locating uniform hyperbolic trajectories, and then used the straddling technique of Miller et al. (1996) to contruct the local invariant manifolds with contour advection (see also Koh & Plumb, 2000). Because of the short persistence times of the geometric structures, the manifolds in general cannot be extended to the point of showing any lobe structure (Figure 4c). However, in the region of largest tropopause deformation, near O¡E, there is a uniform hyperbolic trajectory located on the poleward side of the tropopause, consistent with the picture of strongly supercritical wave breaking discussed in Polvani & Plumb (1992). Here we see the suggestion of a heteroclinic tangle and the associated lobe structure.

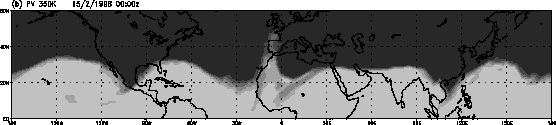
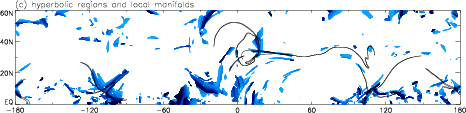
Figure 4: Flow properties at 350K on 15/2/1998: (a) stable (green) and unstable (red) manifolds calculated by the finite strain method; (b) ECMWF analysed PV; (c) uniform hyperbolic trajectories (blue) and their local manifolds calculated by the Jacobian method, and the extended manifolds calculated by straddling.

Previous: Effective diffusivity Next: Conclusions Up: Ext.