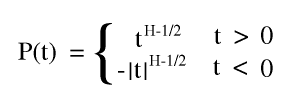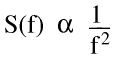
The purpose of this applet is to demonstate simple one dimensional fractional Brownian motion (fBm).
The most familiar context of Brownian Motion is probably that of a random walk. Here a object "picks" a direction to walk in at random and travels a distance given by a Gaussian distribution. The resulting path is Brownian motion. Brownian Motion or Brownian Noise, then, is the unpredictable changes in a quantity, say V, with respect to time.
Brownian Noise is distinguished from other types of noise (white noise, for example) by its spectral distribution, SV(f). SV(f) corrosponds roughly to the mean square fluctuations at a particular frequency and in Brownian noise SV(f) varies as (1/f)^2 when plotted on a log-log scale.
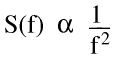
White noise by contrast has a spectral distribution with no dependance on frequency.
Brownian Motion can also be described with a parameter H. As the applet illustrates the value of H affects the smoothness of the graph. Formally, fractional Brownian Motion or Noise, VH(t) is characterized by the proportionality
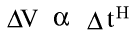
when H = 1/2 the usual Brownian Motion associated with a random walk results.
Brownian Noise can be generated in several ways. This applet uses a random cut method. In order to produce the graphs above for H = 1/2 a series of random cuts are made. These cuts take the form of step functions whose heights area random Gaussian values and whose jump in height occurs at random times. The Brownian noise is constucted throught the addition of many random cuts in the process illustrated below. After this first cut is made another is made at another random time yielding the addition of the two step fuctions
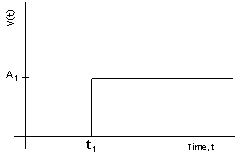
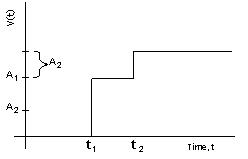
This can be stated mathemtically as follows
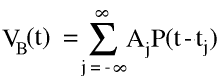 where
where 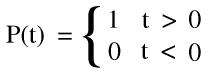
For the case where H varies from the value of 1/2 we simply use random cuts that have a different probability distribution such that