Bernoulli Shift

The Bernoulli shift is a simple example which contains many of the concepts which characterise chaos as a whole.

These points include Devaney's (1992) definition of chaos:

1) the periodic orbits are dense,

3) the system is sensitive to initial conditions.

The three examples below demonstrate the various aspects of chaos that can be derived from the above definition and are properties of all chaotic systems.

How the Bernoulli shift works:

The Bernoulli shift, like all chaotic systems, starts with an initial parameter, transforms this parameter, and then uses this transformed parameter for the input of the next iteration. In this case the parameter is an image. The transformation, itself, consists of four steps (Blume and Reinhardt (1997)):

1)start with a unit square [0,1]x[0,1],

2)compress the square to one half its size in the y direction and stretch it to twice its size in the x direction,

3)cut the resulting rectangle in the y direction such that its width is halved (ie. cut along x=1),

4)Move the right hand rectangle from step 3) on top of the left hand rectangle.

What is important about the Bernoulli shift?

The Bernoulli shift clearly demonstrates three important characteristics of chaotic systems. It is:

area preserving,

bounded and

deterministic.

Area preservation is extremely important in Hamiltonian systems as Louisville's theorem [Landau and Lifschitz (1970), Goldstein (1976)] guarantees the the preservation of phase-space volume as the system evolves through time.

The transformation is bounded as it is the result of linear transformations. Analytically, the description of this transformation is:

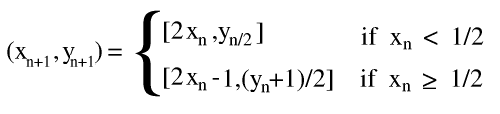
The importance of bounding can be seen in fractals such as the Sierpinsky gasket.

Determinisism is, perhaps, one of the most important features of this mapping. It is completely deterministic yet very sensitive to initial conditions, as the first two examples demonstrate. The sensitivity to initial conditions is what causes the transformation to become unpredictable.

The concept behind the Bernoulli shift is actual from a more general, numeric version call a shift map. The shift map is defined by the equation:

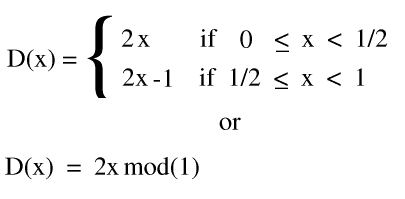
The mapping looks like:

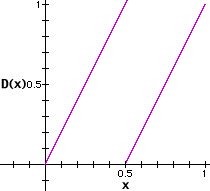
In this case the mapping is often called a shift map because the numbers can be easily manipulated when in binary form. A seed number in the mapping can be represented in the form 0.1010010... To apply the mapping we multiply by 2. In binary this is done by simply shifting all the numbers over to the left such that we get 1.010010... for our example. To take the modulus we simply drop the integer part so we have 0.010010...

Since a random seed would have any possible complexity. This is what makes it chaotic. The output is indistinguishable from noise even though the process is completely deterministic.

There exists two stationary points in this mapping: 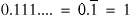and 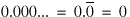. These correspond to completely black or white images in the Bernoulli shift. We can also obtain periodic mappings for numbers such as:. The third example shows this.

Now that you've made it this far you can see what the transformation does with a much larger image. Take note of how few iterations it takes for the image to approach that of noise.