Leibniz-Institut für Atmosphärenphysik ,Schlossstr. 6, 18225 Kühlungsborn,
Germany
email-contact: koernich@iap-kborn.de
FIGURES
Abstract
Introduction
The Arctic Oscillation (AO) describes a sea level pressure (SLP) oscillation between middle and polar latitudes in the northern hemisphere. Thompson and Wallace (1998) defined the AO as the leading empirical orthogonal function (EOF) of the wintertime monthly mean SLP. Accordingly, a pattern in the southern hemisphere was defined as the Antarctic oscillation index (AAO) by Gong and Wang (1999). For both oscillations Thompson and Wallace (2000) introduced the expression Annular Modes (AM), referring to the strong zonal symmetry of the patterns.
In the troposphere, both hemispheres display the AM patterns throughout the year (Thompson and Wallace, 2000). The regression of the AM indexes on the zonal-mean zonal wind shows a latitudinal dipole and resembles the pattern of the zonal index (Thompson and Wallace, 2000). An obvious similiarity connects the AO and the North Atlantic Oscillation (NAO), as is clearly discussed by Wallace (2000).
Another characteristic of the AMs is the vertical extension into the stratosphere. Thompson and Wallace (2000) showed that there exist certain ``active'' months for the stratospheric AM, which comprise the northern hemispheric winter (January to March) for the AO and the southern hemispheric late spring (November) for the AAO.
In this work we focus on how differently forced stationary waves influence variability patterns in troposphere and stratosphere and discuss the results in connection with the AM. In order to specify the different forcing mechanisms, i.e. orography and latent heating, in a straightforward manner, an idealized general circulation model (GCM) from the bottom to the lower mesosphere is employed. This model is described in the next Section 2. The surface pressure variability is examined in Section 3, while Section 4 deals with the activation of the stratospheric AO depending on stationary wave forcing in the lower troposphere. The final Section 5 offers a summary of the results.
Model description
The Kühlungsborn Mechanistic general Circulation Model (KMCM)
(Becker and Schmitz, 2001) is a dry idealized GCM. The model is
run at moderate resolution with triangular truncation at wavenumber
29 in the horizontal and 24 hybrid levels, up to 0.3 hPa. Temperature
relaxation parametrizes the radiation. The relaxation time is
16 days and drops down to 4 days at the upper rim. All simulations
are ``perpetual January''. In the troposphere, relaxation temperature
1![]() corresponds to observational temperature with increased meridional
gradients. In the stratosphere
corresponds to observational temperature with increased meridional
gradients. In the stratosphere ![]() is related to the radiatively determined state.
is related to the radiatively determined state.
In order to examine the influence of different stationary wave
forcing mechanisms, KMCM yields the possibility to turn them on
or off independently. These mechanisms are world orography (![]() ) as well as additional diabatic heating in the deep tropics (
) as well as additional diabatic heating in the deep tropics (![]() ) and middle latitudes (
) and middle latitudes (![]() ):
):
| (1) |
The first term on the l.h.s. is used to mimic convective heating
in the tropics. The second term describes self-induced condensational
heating in middle latitudes in order to mimic land-sea heating
contrasts. It depends linearly on the pressure velocity ![]() and is only active for rising motions due to the Heavyside function
and is only active for rising motions due to the Heavyside function
![]() .
. ![]() and
and ![]() are prescribed functions of longitude, latitude and pressure
(Becker and Schmitz, 2001, their Fig. 2). For a more detailed
model description, including turbulent boundary layer mixing and
definition of the surface temperature, the reader is referred
to Becker and Schmitz (2001).
are prescribed functions of longitude, latitude and pressure
(Becker and Schmitz, 2001, their Fig. 2). For a more detailed
model description, including turbulent boundary layer mixing and
definition of the surface temperature, the reader is referred
to Becker and Schmitz (2001).
The nomenclature of the model runs consists of the three abbrevations
for the forcing mechanisms. By writing them in brackets or as
function of longitude ![]() it is indicated whether the zonal-mean or the longitude-dependent
field is included. Starting from the rotationally invariant reference
run
it is indicated whether the zonal-mean or the longitude-dependent
field is included. Starting from the rotationally invariant reference
run
![]() , orographic (run
, orographic (run
![]() ), midlatitudinal (run
), midlatitudinal (run
![]() ) and tropical thermal forcing of stationary waves(run
) and tropical thermal forcing of stationary waves(run
![]() ) are added and can be combined with each other (e.g. run
) are added and can be combined with each other (e.g. run
![]() ). All mechanisms are present in run
). All mechanisms are present in run
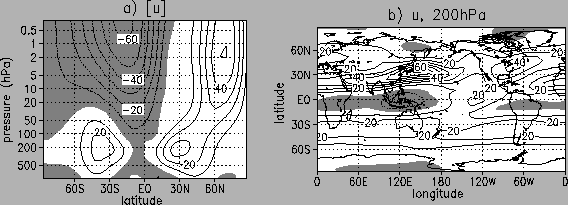
![]() , that generates a realistic mean state of the atmosphere (Fig. 1). The length of each model run is 1801 days.
, that generates a realistic mean state of the atmosphere (Fig. 1). The length of each model run is 1801 days.
Prior to the EOF analysis the model data was smoothed with a binomial
30-day low-pass filter and weighted with the square root of cosine
latitude. The low-pass filter reduced each data set by 128 days.
All EOFs are calculated for the northern hemisphere (![]() N to
N to ![]() N). One-point correlation maps are used for comparison.
N). One-point correlation maps are used for comparison.
 |
Annular Modes in the surface pressure
For every simulation the leading variability patterns of the surface
pressure are AM-like. Fig. 2 shows these patterns for run
![]() and run
and run
![]() . The explained variances of the EOFs are 16.8% and 23.3%. Especially
in run
. The explained variances of the EOFs are 16.8% and 23.3%. Especially
in run
![]() (Figs. 2b,d), the variability pattern and the explained variance of 23.3%
are comparable with results of Thompson and Wallace (1998, their
Fig. 1, 22% explained variance). The main features of their EOF,
besides the strong zonally symmetric component, are the localized
action centres over the Pacific and the Atlantic. These features
can also be found for run
(Figs. 2b,d), the variability pattern and the explained variance of 23.3%
are comparable with results of Thompson and Wallace (1998, their
Fig. 1, 22% explained variance). The main features of their EOF,
besides the strong zonally symmetric component, are the localized
action centres over the Pacific and the Atlantic. These features
can also be found for run
![]() . For the runs with thermal wave forcing alone (not shown) the
variability patterns have a stronger zonally symmetric character,
whereas embedded longitudinal structures are present in the model
runs with orographic wave forcing .
. For the runs with thermal wave forcing alone (not shown) the
variability patterns have a stronger zonally symmetric character,
whereas embedded longitudinal structures are present in the model
runs with orographic wave forcing .
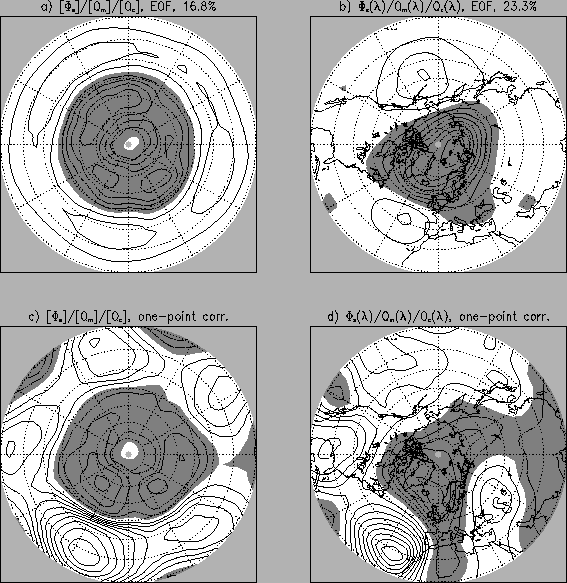 |
The pattern correlation between EOFs and one-point correlation
maps reaches 0.78 for run
![]() and run
and run
![]() . Nevertheless, the physical meaning of surface pressure-EOFs
is open to question (Ambaum et al., 2000). The situation is different
for stratospheric EOFs, as the next section demonstrates.
. Nevertheless, the physical meaning of surface pressure-EOFs
is open to question (Ambaum et al., 2000). The situation is different
for stratospheric EOFs, as the next section demonstrates.
The stratospheric Arctic Oscillation
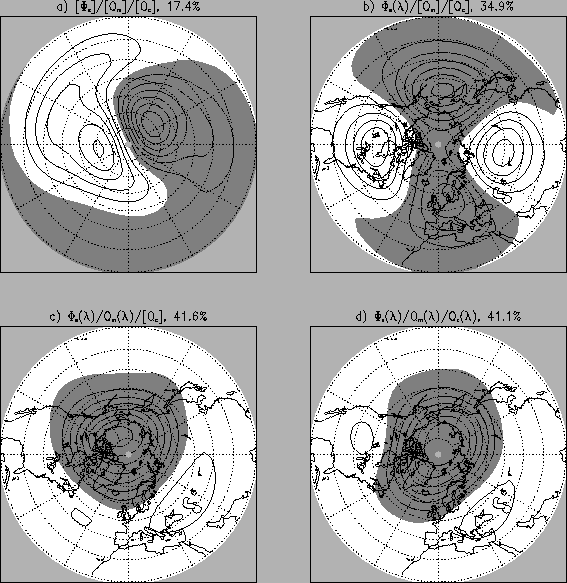
For run
![]() , Fig. 3 shows the first EOF of the 50hPa-geopotential and one-point correlation
maps for two reference points. All three patterns consist of a
comparably strong zonal symmetry and a high pattern correlation
( for a and b: -0.9, for a and c: 0.65). Furthermore, the correlations
between first principle components of 50hPa-geopotential and either
50hPa-zonal wind or 50hPa-temperature reach values greater than
0.9. These results and the high explained variance of the first
50hPa-geopotential EOF (41.6%) seems to indicate that this EOF
represents a physically meaningful variability pattern.
, Fig. 3 shows the first EOF of the 50hPa-geopotential and one-point correlation
maps for two reference points. All three patterns consist of a
comparably strong zonal symmetry and a high pattern correlation
( for a and b: -0.9, for a and c: 0.65). Furthermore, the correlations
between first principle components of 50hPa-geopotential and either
50hPa-zonal wind or 50hPa-temperature reach values greater than
0.9. These results and the high explained variance of the first
50hPa-geopotential EOF (41.6%) seems to indicate that this EOF
represents a physically meaningful variability pattern.
 |
For different stationary wave forcing, the leading EOFs of the
50hPa-geopotential show different features. In particular, in
run
![]() and run
and run
![]() (Figs. 4a,b), the leading EOFs have strong wave components, whereas predominantly
zonally symmetric patterns are obtained in run
(Figs. 4a,b), the leading EOFs have strong wave components, whereas predominantly
zonally symmetric patterns are obtained in run
![]() , run
, run
![]() (Figs. 4c,d) and run
(Figs. 4c,d) and run
![]() (not shown).
(not shown).
But only run
![]() and run
and run
![]() do generate AO patterns (Figs. 4c,d) that agree reasonably well with observational data (Thompson
and Wallace, 2000). This holds for structure as well as explained
variance (here: 41.6% and 41.1%, theirs: 54%). In the other runs
such a mode cannot be found even in the higher EOFs. Therefore,
the combination of orographic and middle latitude thermal wave
forcing seems to be imperative for the activation of an AO-like
variability pattern in the stratosphere. Thermal wave forcing
in the tropics does not contribute conspicuously to this variability
mode in our model.
do generate AO patterns (Figs. 4c,d) that agree reasonably well with observational data (Thompson
and Wallace, 2000). This holds for structure as well as explained
variance (here: 41.6% and 41.1%, theirs: 54%). In the other runs
such a mode cannot be found even in the higher EOFs. Therefore,
the combination of orographic and middle latitude thermal wave
forcing seems to be imperative for the activation of an AO-like
variability pattern in the stratosphere. Thermal wave forcing
in the tropics does not contribute conspicuously to this variability
mode in our model.
 |
Using the first principle component of the 50hPa-geopotential, a composite analysis is carried out with 10% of the days with the lowest and highest values of the principle component. In a negative (positive) phase an anomalous high (low) geopotential prevails at the pole, together with a weakened (strengthened) polar vortex. We call the ensemble difference between the negative and positive phase the stratospheric phase anomaly. In the following, we discuss its zonal-mean fields focussing on the runs with orographic and middle latitude thermal stationary wave forcing.
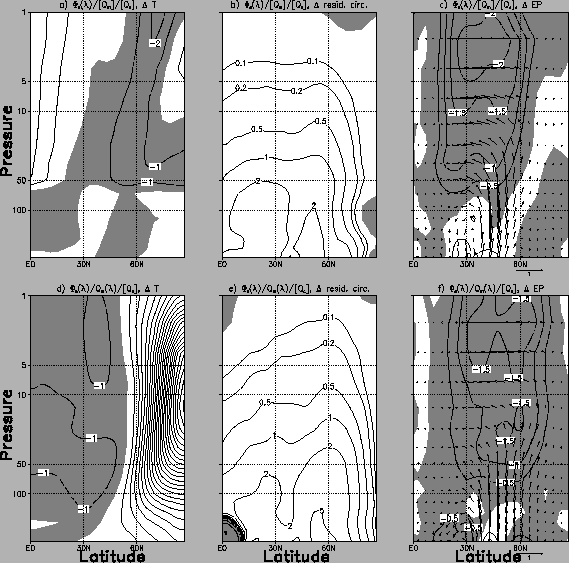 |
In run
![]() , phase anomalies of temperature (Fig. 5d) and residual mass circulation (Fig. 5e) prove that, during the negative phase, the anomalous weak polar
vortex coincides with a warming of the polar stratosphere and
an enhanced residual circulation. No such relation exists, if
only one forcing mechanism is present (run
, phase anomalies of temperature (Fig. 5d) and residual mass circulation (Fig. 5e) prove that, during the negative phase, the anomalous weak polar
vortex coincides with a warming of the polar stratosphere and
an enhanced residual circulation. No such relation exists, if
only one forcing mechanism is present (run
![]() (not shown) and run
(not shown) and run
![]() (Figs. 5a,b)). In those runs we rather find that an anomalous weak polar
vortex is accompanied by cooling in high latitudes and warming
in the subtropical stratosphere, while the residual circulation
amplifies weakly.
(Figs. 5a,b)). In those runs we rather find that an anomalous weak polar
vortex is accompanied by cooling in high latitudes and warming
in the subtropical stratosphere, while the residual circulation
amplifies weakly.
The anomalous Eliassen-Palm(EP)-flux divergence in run
![]() (Fig. 5f) indicates an enhanced planetary wave activity in the polar
night stratosphere during the negative phase. Even though such
a phase anomaly is principally also observed in run
(Fig. 5f) indicates an enhanced planetary wave activity in the polar
night stratosphere during the negative phase. Even though such
a phase anomaly is principally also observed in run
![]() (Fig. 5c) and run
(Fig. 5c) and run
![]() (not shown), the effect is weaker and concentrates in subtropical
latitudes.
(not shown), the effect is weaker and concentrates in subtropical
latitudes.
Conclusions
We examined the influence of differently forced stationary waves on variability patterns of the troposphere and stratosphere in an idealized GCM.
As concerns the surface pressure variability, the Annular Mode depends weakly on the kind of the forcing mechanism. While land-sea heating contrasts enhance the development of a zonally symmetric mode, orography enables the embedding of a planetary-wave pattern and leads to some weakening of the explained variance. Nevertheless, our model runs demonstrate that the AM is the dominant variability mode for any or even no stationary wave forcing.
The situation in the stratosphere is contrasting. Only the combination
of orographic and midlatitude thermal wave forcing activates an
AO pattern in the stratosphere. In run
![]() , the stratospheric AO composites of temperature and residual
mass streamfunction show a strong connection. During the phase
with a weakened polar vortex, the amplified residual circulation
is driven by an enhanced wave activity in the polar stratosphere,
that is manifest in the EP-flux divergence. The anomalous EP-flux
divergence extends into the polar stratosphere and thereby enables
the variability mode.
, the stratospheric AO composites of temperature and residual
mass streamfunction show a strong connection. During the phase
with a weakened polar vortex, the amplified residual circulation
is driven by an enhanced wave activity in the polar stratosphere,
that is manifest in the EP-flux divergence. The anomalous EP-flux
divergence extends into the polar stratosphere and thereby enables
the variability mode.
Besides the activation of the stratospheric AO, also the climatological residual circulation extends to the polar night stratosphere, only if both orography and land-sea heating contrasts are included (Becker and Schmitz, 1999, their Fig. 4).
Bibliography
Back to
| Session 1 : Stratospheric Processes and their Role in Climate | Session 2 : Stratospheric Indicators of Climate Change |
| Session 3 : Modelling and Diagnosis of Stratospheric Effects on Climate | Session 4 : UV Observations and Modelling |
| AuthorData | |
| Home Page | |