Looking for the treasure on the island ...

The notes below are a ``look from aside'' at the problem #64 of Ch. 1 of the textbook (Serway & Jewett).

In short: the problem asks you in the first part to find the co-ordinates of the digging point (the method of searching it is given). In the second part you are asked to show that the location of the point (the co-ordinates to be more explicit) do not depend on the tree with which you start the search algorithm of the digging point.

Here I am going to look at the second part of the problem. I will argue that the location of the digging point can be interpreted as the center of mass of equal-mass trees. Hence, the location of the digging point (read, center of mass) relative to the trees does not depend on the order of counting (labeling) the trees (i.e., what the problem asked us to clarify).

To get there, let us review the method of finding the digging point. The recipe: one starts from tree A and moves toward tree B, but stops at 1/2 of the distance between A and B. Let us call this point ``1''.

Next, one has to move from point 1 toward tree C and go only up to the point which is 1/3 of the $\mathbf{1}\leftrightarrow\mathbf{C}$ distance from 1. Let us call this point 2. And so on .... for the trees D and E. See Fig. 1 for a schematics of the search (with only four trees)

Figure 1: The search algorithm. See text for details.

Imagine now that instead of trees we have a configuration of equal-mass bodies, with given and fixed locations (as are the trees). We denote the bodies as the trees (A, B, etc.) and their common mass by $m$.

By going half-distance between A and B we actually located the center of mass (henceforth denoted as $\mathcal{CM}$) of the two equal-mass bodies. I guess this is kind of obvious. Note that I am not using any fancy/rigorous formalism, no vectors, just everyday language (sic!) - like ``$\mathcal{CM}$'', right(?).

The following statement is kind of half-obvious, but I will prove it is correct at the end of this document (by using the definition of $\mathcal{CM}$ and some vector algebra).

For now, let me assume that the bodies A and B act, for the rest-of-the bodies, as a single body of mass $2m$ located at the position of their $\mathcal{CM}$ (i.e. point 1). The meaning of ``act'' is a bit unclear; let's just assume that the above mentioned ``act'' is for the purpose of finding the center of mass of the whole ensemble of trees-bodies.

Assuming you buy my argument (just kidding, I'll prove it to you!) then by going 1/3 of the distance from point 1 to C we find the $\mathcal{CM}$ of the system which consists of the ``virtual'' body of mass $2m$ located at point 1 and the body of mass $m$ located at C. That location is point 2.

So, to recap: by going 1/2 of the distance from A to B we found the center of mass of the A+B system. Then, by going 1/3 of the distance between 1 and C we located the $\mathcal{CM}$ for the system A+B+C and its location is point 2.

Obviously, by going from 2 toward D and fetching only 1/4 of the $\mathbf{2}\leftrightarrow\mathbf{D}$ distance we get to the point 3 which is $\mathcal{CM}$ of the system A+B+C+D. And so on.

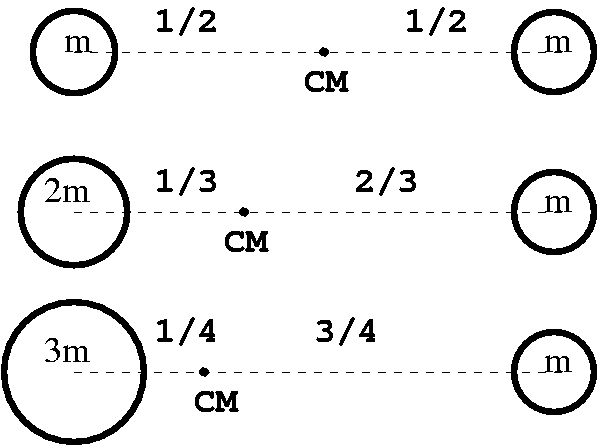
The key step here was to go 1/2, 1/3, 1/4 ...of the corresponding distances. Perhaps, this would be the method used in ancient times to find the center of mass (I might be wrong though). Take a look at Fig. 2 to see graphically where the $\mathcal{CM}$ is located for various mass combinations.

Figure 2: The relative position of the center of mass (CM) for different mass combinations. The ratios 1/2, 1/3, etc... are fractions of the distance between the bodies.

Now, let us summarize our findings. The method indicated by the pirate on the map looks a lot like finding the center of mass of an ensemble of equal-mass bodies. See above. The rigorous solution (see the solution of the homework 1, posted on the web) suggests (and it is true) that this property - the $\mathcal{CM}$ is the digging point -- holds even if the geometry of the problem is not 2-dimensional. It holds in 3-D as well. Talk to me in the tutorial if you find the previous statement hard to comprehend.

Relative to the bodies in the ensemble (their positions are fixed - as are the trees) the position of the $\mathcal{CM}$ is the same regardless of

1. the order in which we label the trees (bodies)
2. the co-ordinate system used to derive the location of the center of mass

Of course, by changing the co-ordinate system the numbers for the coordinates may change, but geometrically speaking the $\mathcal{CM}$ is at a given and unchanged place relative to the ensemble (attention: it is vital that the trees/bodies do not move relative to each other!). Think of the ensemble of trees as of a chemical model of a molecule (with fixed length rods connecting molecules). The co-ordinate system is just like a sheet of paper which can be moved underneath the above rigid construction. The position of the center of mass of the ensemble relative to the trees/bodies obiviously doesn't depend on how we move the paper.

Since the digging point is the center of mass, the second part of the problem is answered by the above enumeration and subsequent explanations.

Finally, I have a promise to keep: to prove to you that finding the $\mathcal{CM}$ of the ensemble A+B+C is the same as finding the $\mathcal{CM}$ of the system consisting of point 1 (which harbors a ``virtual'' body of mass $2m$) and point C (of mass $m$).

By definition (well, I am not sure; this might be just a consequence of the definition) the position of the center of mass of a ensemble of bodies is given by

$$\vec{r}_{\mathcal{CM}} = \frac{m_1 \vec{r}_1 + m_2 \vec{r}_... ...vec{r}_3 + m_4 \vec{r}_4 +\dots } {m_1+m_2+m_3 +m_4 + \dots},$$ (1)

where $(m_1,\vec{r}_1)$ a.s.o. are the mass and the position vector of the body #1, a.s.o. This definition, applied to the case of three bodies gives

$$\vec{r}_{\mathcal{CM}} = \frac{m_1 \vec{r}_1 + m_2 \vec{r}_2 + m_3 \vec{r}_3 } {m_1+m_2+m_... ...le\frac{m_1 \vec{r}_1 + m_2 \vec{r}_2}{m_1+m2}} + m_3 \vec{r}_3 } {m_1+m_2+m_3}$$ (2)

$$= \frac{ (m_1+m_2)\vec{r}_{1,2} + m_3 \vec{r}_3} {m_1+m_2+m_3}.$$ (3)

Above, I denoted by $\vec{r}_{1,2}$ the vector pointing to the center of mass of the ensemble ($m_1$, $m_2$).

Obviously, we solved the general case. For our particular problem, where all masses are equal, we get

$$\vec{r}_{\mathcal{CM}} = \frac{2m\vec{r}_{1,2} + m \vec{r}_... ...ac{1}{3}\vec{r}_{\mathbf{C}} +\frac{2}{3}\vec{r}_{\mathbf{1}}.$$ (4)

Above I switched notation back to point 1 and tree C to make the link to our problem more clear. We see now what is the origin of those ``magic'' 1/2 , 1/3, 1/4 steps. It just follows from the definition of center of mass.

As you probably already know, the position of the digging point is given by (see the web-posted solution)

$$\vec{F} = \frac{1}{5}\left(\vec{A}+\vec{B}+\vec{C}+\vec{D}+\vec{E}\right),$$ (5)

where $\vec{A},\vec{B} \dots$ are the vectors pointing to the position of trees A, B .... In my notation $\vec{F}$ is the position of the digging point -- all these vectors have their origin at point O (see the map of the pirate). I believe it is clear by now that the above expression is just a particular case (with $m_1 = m_2 = \dots =m_5 =m$) of the definition (1).