For a printer-friendly version of this text please use the PDF version. Two pages, 50kbytes.

This document deals with the physics (actually, the math) of an experiment demonstrated during the lecture.

By popular demand (read: judging by the response in the tutorials, none of you have tried to do the problem at home!) I thought that posting the solution would be of some help.

The setup (re: D. Harrison demonstration) is:
A $m=57g$ tennis ball is held above a $M=590g$ basketball, and both are released from rest when the bottom of the basketball is $H=1.20m$ above the ground. Assume the basketball instantaneously reverses its velocity when it hits the ground and that at this moment the tennis ball is still moving down. The basketball then collides with the tennis ball, causing it to rebound. How high does the tennis ball go?

In what follow I am presenting the calculation of the bouncing height for the tennis ball.

First, here is a picture of the setup.

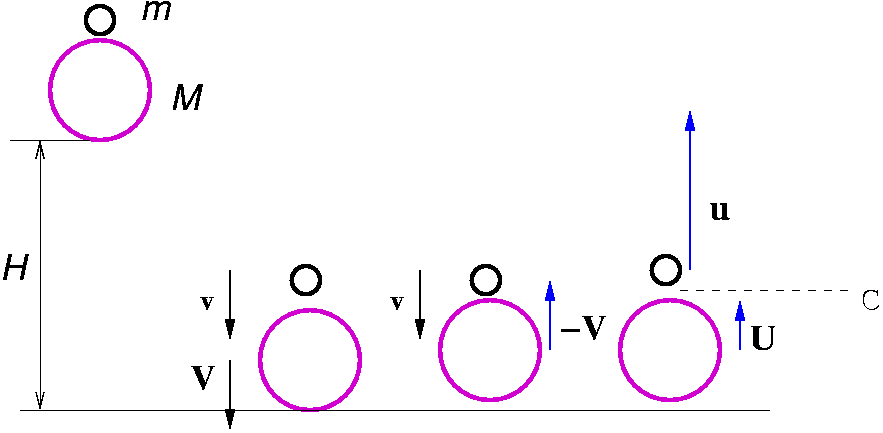
On the diagram, $m, \ M$ are the masses of the balls, $H$ is the height (note that both balls fall the same distance, $H$, assuming negligible deformations during the impacts), $\mathbf{v}, \mathbf{V}$, and $\mathbf{u}, \mathbf{U}$ are the velocities of $m$ and $M$ before and after the collision, respectively. Note the use of boldface, instead of $\vec{()}$ to denote vectors on the diagram.

To simplify our lives, let us assume the collisions are perfectly elastic. Hence, the kinetic energy is conserved. Total momentum of the (tennis ball + basketball) system is conserved during the collision (this is true if one assumes, reasonably, that the impulse of external forces acting on the system is negligible during the collision time). The momentum conservation for the whole system right before and right after the collision gives

$$m\vec{v} + M(-\vec{V}) = m\vec{u} + M\vec{U}.$$ (1)

Note that the velocity of the basketball is $-\vec{V}$, because of the perfectly elastic ``reflection'' of the ground. From the kinetic energy conservation we get

$$\frac{1}{2}mv^2 + \frac{1}{2}MV^2 = \frac{1}{2}mu^2 + \frac{1}{2}MU^2.$$ (2)

For convenience, I use arrows instead of boldface, to denote vectors in the text.

Now, let us choose ``upward'' to be the positive direction for the velocities. Then, equation (1) gives us

$$-mv + MV = mu + MU.$$ (3)

Note that we expect $v, V, u, U$ to be positive quantities (that's why I put ``by hand'' the signs as they are in (3)).

N.B. The sign of $U$ is not known ``a priori'', and the sign of $u$ is also not known, but for $u$ we assume it is $+$ for the problem to make sense). At the end, if we obtain a positive quantity for $U$ then we know choosing $+MU$ was OK. If not, well, it means the basketball moved the other way.

For now we are interested in $u$ but not $U$. Let's get rid of $U$, by expressing it from (3) and substituting into (2). We have

$$U = V - \alpha ( v + u ),$$ (4)

where, for reasons of simplicity I denoted

$$\alpha \equiv \frac{m}{M}.$$

N.B. Introducing $\alpha$ makes the ``picture'' cleaner and clearer, and calculations less prone to errors. Besides, in this problem $\alpha$ is the main control parameter. See below.

Finally, by dividing through with $M$ in (2) and using (4) one obtains

$$\alpha v^2 + V^2 = \alpha u^2 + \left( V -\alpha ( v + u ) \right)^2.$$ (5)

At this point it seems we end up with a quadratic equation for $u$. A closer inspection of (5) reveals an easier path:

$$v^2 - u^2 = \alpha(u+v)^2 - 2V (u+v),$$ (6)

which, in the case $v+u \neq 0$ (true, since we expect $u, v > 0$), simplifies to the linear equation

$$v - u = \alpha(u+v) - 2V,$$ (7)

and hence

$$u = \frac{2V + v(1-\alpha)}{1+\alpha}.$$ (8)

We are done! Almost.

In our case $v =V = \sqrt{2gH}$, and $\alpha \approx 0.0966$.

In the gravitational context (projectile motion, potential/kinetic energy, etc.) the height a given object may reach scales as the square of velocity, that is we have $H \propto v^2$ and $h \propto u^2$.
Of course, you can do it the old way (no need for ``$\propto$'' arguments ...); once you have the value of $u$, the height tennis ball reaches is given by $h = u^2 /2g$ (use Galileo's formula, for example).

Oops, I forgot to mention $h$ is the height to which the tennis ball rebounced after collision - $h$ is measured relative to the collision point, i.e. level ``C'' on the diagram).

Therefore, 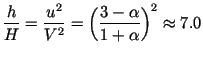$$\frac{h}{H} = \frac{u^2}{V^2} = \left(\frac{3-\alpha}{1+\alpha}\right)^2 \approx 7.0$$. With $H = 1.2m$ we get $h \approx 8.4m$. Impressive!

N.B. There is a danger lurking in this quicky scaling solution. Notice that for $\alpha > 3$ the quantity in the parentheses in the last expression becomes negative. For such values of $\alpha$ the problem doesn't make sense - the tennis ball doesn't bounce back! Do it the ``old way'' to convince yourself of this. The scaling should have read in fact $$\frac{\sqrt{h}}{\sqrt{H}} = \frac{u}{V}$$, which makes it obvious that something is wrong if $$\frac{u}{V} < 0$$.

Revised: 10/21/05 © 2005 Sorin Codoban

For a printer-friendly version of this text please use the PDF version. Two pages, 50kbytes.