Previous : The meridional circulation in a zonally symmetric model Next: Summary Up: Ext. Abst.

 

4. The effects of nonlinearity, of model diffusion, and of the seasonal cycle

To isolate the different mechanisms potentially responsible for the low-latitude upwelling response, we consider a simple idealization of the form of the zonal body force. From here on this is given a compact form with a maximum of ${\bar F}$ at a variable latitude, ${\phi_0}$, and decaying smoothly to zero 15$^\circ$ on either side:

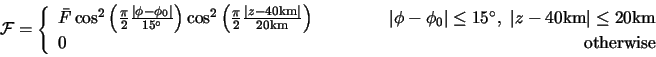\begin{displaymath} \mathcal{F}= \left\{\begin{array}{lcr} {\bar F} \cos^2\left(... ...rt\le20\mbox{km} \\ 0 & & \mbox{otherwise} \end{array}\right. \end{displaymath} (3)


Note also the z-dependence, which is zero below 20km. We choose an amplitude of ${\bar F}=-2$m/s/day, as being physically reasonable in terms of the response produced. This is reduced by up to a factor of 100 in selected experiments below to isolate linear properties of the model response. The radiative relaxation rate is increased to 1/(10 days) and the ``annual cycle'' is reduced to 200 days to reduce the model run-time. Finally, note that the form of the radiative basic state is adjusted slightly to be antisymmetric between hemispheres; this is simply so we can use a basic state that corresponds to a resting atmosphere as the annual average of the seasonally varying basic state. Figure 3 illustrates different upwelling responses for forcing centred on ${\phi_0}=40^\circ$, $30^\circ$, $25^\circ$ and $20^\circ$, for the case of steady forcing and steady radiative basic state (no seasonal cycle) corresponding to a resting atmosphere. Note the significant low-latitude upwelling obtained for ${\phi_0}\le25^\circ$.

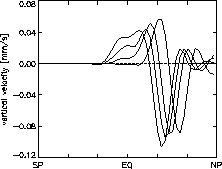
Figure 3: Residual vertical velocity of the zonally symmetric model forced with the compact zonal momentum force with (moving equatorward) ${\phi_0}=40^\circ$, ${\phi_0}=30^\circ$, ${\phi_0}=25^\circ$, ${\phi_0}=20^\circ$.

a. Model hyperdiffusion and vertical viscosity

In considering the latitudinal scale of an induced upwelling response to given forcing it is useful to consider simple scaling arguments. Using similar analysis to that used in Holton et al. (1995) and Garcia (1987) the linearized transformed Eulerian mean equations on the sphere, with a frictional force, $-\kappa u$ in the zonal momentum equation, leads to a steady state relation of the form

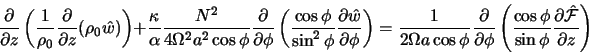\begin{displaymath} \frac{\partial}{\partial z}\left(\frac{1}{\rho_0}\frac{\part... ...{\sin\phi} \frac{\partial\hat{\mathcal{F}}}{\partial z}\right) \end{displaymath} (4)


where $\kappa$ is the friction time-scale, $\alpha$ is the radiative time-scale, and other variable are as in Holton et al. (1995). If the frictional term is replaced by a hyperdiffusion of the form $-\nabla^8u$ (as in our model), then $\kappa$ in (4) can be replaced by ${\gamma_{\max}}\delta^8$, where ${\gamma_{\max}}$ is the rate at which the smallest wave-numbers are damped, and $\delta$ is their lengthscale (ie. the grid resolution). Balancing terms of (4) outside the forcing region leads to horizontal length scales

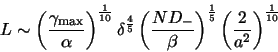\begin{displaymath} L\sim \left(\frac{\gamma_{\max}}\alpha\right)^{\frac1{10}} \... ...}}\beta\right)^{\frac15} \left(\frac2{a^2}\right)^{\frac1{10}} \end{displaymath} (5)


in mid latitudes and

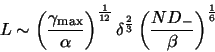\begin{displaymath} L\sim \left(\frac{\gamma_{\max}}\alpha\right)^{\frac1{12}} \... ...\frac23} \left(\frac{N D_{\mbox\tiny -}}\beta\right)^{\frac16} \end{displaymath} (6)


in low latitudes, where $a\sin\phi$ has been approximated by a/2 and L respecitively, and where $D_{\_}=\sqrt{\min(HD,D^2)}$, with D a vertical lengthscale. In both cases, L is the scale on which an upwelling response decays away from the forcing region. Note that the dependence on ${\gamma_{\max}}$ is very weak, so that moderate changes in the hyperdiffusion will have little effect. On the other hand a bigger effect can be expected from moderate changes in the resolution $\delta$. Figure 4a shows the effect of changing the resolution from 31 (solid line) to 64 (dash-dotted line) meridional modes for the case of ${\phi_0}=25^\circ$. The narrowing of the spreading of the response is in good agreement with (5) in midlatitudes but not at low latitudes, where there is little change between the two resolutions.

One possible reason for the above disagreement is the deviation from the vertical of contours of constant angular momentum in low latitudes, induced by the nonlinear zonal momentum forcing. To investigate this, a series of (nearly) linear experiments are presented in Figure 4b with forcing 1/100th that used in Figure 4b, and horizontal resolution of 31 modes (solid) or 64 modes (dash-dotted line) as above. Now, the high resolution case shows a similar narrowing of the response at both high and low latitudes, in contrast to the nonlinear case. We conclude, therefore, that while the hyperdiffusion must certainly play an important role in upwelling response, the mechanism is fundumentally nonlinear. Note also that although the linear forcing is 1/100th that of the nonlinear, the response is reduced only by a factor of 1/50. Finally is interesting to note the response when the hyperdiffusion is zero, but including a vertical viscosity of 1m/s/s. Again this gives a non-zero tropical upwelling response, though with a different form than that obtained with hyperdiffusion.

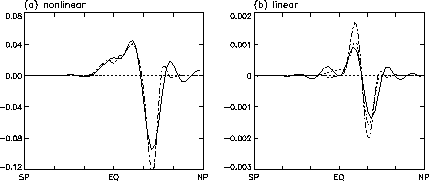
Figure 4: As Figure 3 with ${\phi_0}=25^\circ$: (a) nonlinear forcing ( ${\bar F}=-2\times10^{-5}$m/s/s) with 31 meridional modes (solid) and 64 meridional modes (dot-dashed); (b) linear forcing ( ${\bar F}=-2\times10^{-7}$m/s/s) and frictionless (dotted), with hyperdiffusion only (solid), and with vertical viscosity only (dashed).

 

b. The seasonal cycle

When the zonal velocity basic state is not that of a resting atmosphere, angular momentum contours are again distorted from the vertical, this distortion being more pronounced at low latitudes. The distortion can have a significant impact on the upwelling response, as can be seen in Figure 5a, for a linear case with steady forcing and radiative basic state corresponding to a resting atmosphere (dotted) and to a perpetual winter (solid). In midlatitudes the change in angular momentum distribution has the effect of shifting the upwelling/downwelling response equatorwards, resulting in a response similar to that which would be obtained by retaining the resting atmosphere basic state and introducing an equatorward displacement of the forcing region. The effect at low latitudes can be then understood in terms of this apparent equatorward displacement, which results in an increased tropical upwelling (cf Figure 3). We may therefore expect that when a realistic seasonal cycle is included in the radiative basic state the upwelling response be modified. (Recall that such a modification was already apparent in Figure 2b.) Further, from (1) we see that nonlinear interactions between the time varying components of meridional velocity, v', and the latitudinal gradient of the momentum, $m'_\phi$, in ${\mathcal J}$ can act to produce a non-zero time-averaged response away from the forcing region.

Figure 5b and Figure 5c show the change in response between the annually averaged seasonally varying response (solid) and the steady state response to forcing values equal to the annaully averaged thermal and momentum forcing (dotted), for linear and nonlinear momentum forcing respectively. Equation (1) can help explain the equatorward shift in the midlatitude seasonally varying response, however it may not be used at the equator, where angular momentum contours fail to span the vertical. Here, as in the recent study by Plumb & Eluzsliewicz (1999), it seems that the very small zonal forces generated by the model diffusion are sufficient to create an upwelling response that penetrates well into the opposite hemisphere. Figure 5bc does suggest however that the nonlinear interaction implied by (1) is sufficient to shift the apparent forcing latitude equatorwards, with the result that the small diffusive forces and hence the upwelling response are increased at low latitudes.

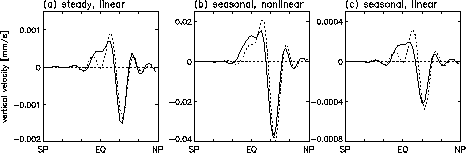
Figure 5: As Figure 3 with ${\phi_0}=25^\circ$: (a) steady state response to linear forcing with a radiative basic state corresponding to a resting atmosphere (dotted) and a perpetual winter (solid); (b) annually averaged response seasonally varying forcing and heating (solid) and the corresponding steady state response to steady forcing and heating (dotted), with nonlinear forcing; (c) as (b) but with linear forcing.

Previous : The meridional circulation in a zonally symmetric model Next: Summary Up: Ext. Abst.