Previous: Observation and data analysis Next: Summary Up:Ext. Abst.

 

3. Gravity wave characteristics

     For the analysis of the seasonal variation of gravity wave activity, monthly mean gravity wave energy densities, $ E_0$ and $ E_t$, are calculated in the stratosphere and the troposphere. $ E_0$ and $ E_t$ are given by

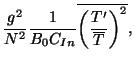$\displaystyle E_0$ $\displaystyle =$ $\displaystyle \frac{g^2}{N^2} \frac{1}{B_0 C_{In} } \overline{ \bigg(\frac{T'}{\overline{T} } \bigg)^2 } ,$ (1)
$\displaystyle E_T$ $\displaystyle =$ $\displaystyle \frac{1}{2} \left[ \overline{u'^2} + \overline{v'^2} + \frac{ g^2}{N^2} \overline{ \bigg(\frac{T'}{\overline{T} } \bigg)^2 } \right] ,$ (2)

where $ B_0$ and $ C_{In}$ can be derived using three-dimensional gravity wave spectrum model suggested by Fritts and VanZandt (1993).
     Figure 2 shows time series of monthly mean $ E_t$ and $ E_0$ in the stratosphere and the troposphere. Although gravity wave energy $ E_0$ are derived in the vertically uniform basic state zonal wind and static stability, the magnitude and tendency of $ E_T$ and $ E_0$ in the stratosphere are almost the same. However, $ E_T$ is quite different from $ E_0$ in the troposphere. The similarity between $ E_T$ and $ E_0$ in the stratosphere suggests that the calculated perturbation variables in the stratosphere can be referred to as gravity wave perturbations.

Figure 2. Time series of monthly mean $ E_T$ and $ E_0$ in (a) the stratosphere and (b) the troposphere. In each panel, $ E_T$ and $ E_0$ are plotted with solid and dash lines, respectively.
\includegraphics[scale=0.60]{fig02}

     In the stratosphere, $ E_T$ is much larger in January and November than in the other months. The gravity wave activity in the stratosphere can be controlled by the basic state flow and the characteristics of wave sources. The stationary mountain waves can propagate vertically into the stratosphere in winter because they do not meet critical level for the zonal wind structure in the troposphere(Figure 1b). However, those stationary waves can not propagate into the stratosphere in summer because of the reversed zonal wind near the tropopause. For the summer zonal wind structure, non-stationary waves induced by convective storms may not propagate into the stratosphere, either. Thus the strong wave activity in the winter stratosphere can be determined by the combination of the above-mentioned wave sources and basic state flow conditions.
     In the atmosphere, there are many possible sources for gravity waves besides mountain and convection. Kitamura and Hirota(1989) showed the relevance of the subtropical jet to the wave activity through the anaysis of the propagation direction of waves. Their study suggests that the observed gravity waves in this study are generated near the subtropical jet region far away form Pohang. Accordingly, wave propagation characteristics should be estimated in order to precisely analyze the strong gravity wave activity in the winter stratosphere. However, the spectral characteristics and dominant spatial and temporal scales of gravity wave should be calculated in advance in order to estimate wave propagation characteristics.
     In this study, we calculated the power spectral densities of the normalized temperature as a function of the vertical wavenumber. Allen and Vincent (1995) fitted their model spectra into the monthly mean PSD to obtain several spectral characteristics of gravity waves. The model spectra used in Allen and Vincent is given by

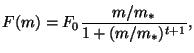$\displaystyle F(m) = F_0 \frac{ m/m_* }{ 1 + (m/m_* )^{t+1} },$ (3)

where $ m$ is vertical wavenumber( $ = 1/ \lambda_z $), $ m_*$ is the characteristic vertical wavenumber( $ = 1/{\lambda_z}_*$), and $ t$ is the log-scale spectral slope in the large vertical wavenumber region.
     The characteristic vertical wavenumber($ m_*$) indicates the dominant vertical scale in the observed gravity wave field because the gravity wave energy is concentrated near the vertical scale corresponding to $ m_*$ in the area-preserving form of PSD(not shown).  Yearly mean $ m_*$s are $ 2.29 \times 10^{-4}$(4.37 km) and $ 2.55 \times 10^{-4}$(3.92 km) in the stratosphere and the troposphere, respectively. The spectral slopes($ t$) of monthly mean PSDs in the large vertical wavenumber region are slightly less than -3 except for the stratospheric PSD in May, July, and August. Yearly mean $ t$ are 2.66 and 2.86 in the stratosphere and the troposphere, respectively.
     The intrinsic frequency and mean propagation direction of the wave are estimated using Stoke's parameter method(Eckermann and Vincent 1989) and Hilbert transform, and mean horizontal and vertical wavenumber are obtained assuming that the observed perturbation variables are due to inertia gravity waves. The monthly mean vertical wave lengths are about 2.94 km and 2.55 km in the stratosphere and the troposphere, respectively. The estimated monthly mean horizontal wave lengths are about 430.94 km and 96.59 km in the stratosphere and the troposphere, respectively. Thus it can be immediately seen that the horizontal scales of waves are, on average, 200 times as large as the vertical scales of waves in the stratosphere. The ratio of intrinsic frequency to inertia frequency ( $ = \hat{\omega} / f $) are about 2.26 with small seasonal variations in the stratosphere. The intrinsic phase speed and group velocity are written as

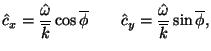$\displaystyle \hat{c}_x = \frac{ \hat{\omega}}{\overline{k}} \cos \overline{\phi} \qquad \hat{c}_y = \frac{\hat{\omega}}{\overline{k}} \sin \overline{\phi} ,$ (4)
$\displaystyle c_{gx} \approx \overline{u} + \hat{c}_{x} \qquad c_{gy} \approx \overline{v} + \hat{c}_{y} ,$ (5)

where  $ \displaystyle \hat{\omega}$ is the intrinsic frequency,  $ \displaystyle \overline{k}$ is mean horizontal wavenumber, and  $ \displaystyle \overline{\phi}$ is mean propagation direction.
     Figure 3 shows the intrinsic phase velocity and group velocity vectors in the stratosphere in January and July. In the stratosphere, the mean direction of intrinsic phase velocities in winter is mainly toward the northwest, while that in summer is toward the northeast. That is, the observed gravity waves in the stratosphere have the anisotropic propagation characteristics. The monthly mean  $ {\hat{c}}_{ix}$s in the stratosphere show an interesting seasonal variation that there exist the negative $ {\hat{c}}_{ix}$ in winter, and positive in summer.  In the troposphere, however, the propagation characteristics do not have the anisotropy that exists in the stratosphere.

Figure 3. The intrinsic phase velocity and group velocity vectors in the stratosphere in January and July.
\includegraphics[scale=0.60]{fig04}

     The monthly mean $ c_{gx}$ shows the seasonal variation opposite to that of  $ {\hat{c}}_{ix}$ in the stratosphere. Thus we can see that the basic state wind significantly affects the dominant direction toward which the gravity wave energy propagates.
     In this study, because $ w'$ is not directly observed, the zonal and meridional momentum fluxes are indirectly estimated in order to examine the interaction between the observed gravity waves and the large-scale circulation. the zonal and meridional momentum fluxes are calculated using

$\displaystyle \overline{\rho} \overline{u' w'} = \frac{\overline{\omega} g}{N^2} \overline{ u' \hat{T}'_{+90} } \delta_- ( \overline{\omega} ),$ (6)
$\displaystyle \overline{\rho} \overline{v' w'} = \frac{\overline{\omega} g}{N^2} \overline{ v' \hat{T}'_{+90} } \delta_- ( \overline{\omega} ),$ (7)

where  $ \displaystyle \overline{\omega} $ is the spectral average value,  $ \hat{T}'_{+90}$ is the Hilber transformed normalized temperature perturbation, and  $ \displaystyle \delta_- (\omega)= 1 - \bigg\{ 1 - \bigg(\frac{f}{\omega} \bigg) \bigg\}$.

     From the monthly mean zonal and meridional momentum flux in the stratosphere, we can see a clear seasonal variation of zonal momentum flux. In the stratosphere, zonal momentum is transported downward in winter, while that is transported upward in summer.
     Because the intrinsic phase velocities in the winter stratosphere are mainly westward, the downward trasfer of the zonal momentum should be observed for the gravity waves that propagate their energy upward. Thus it is expected that the gravity waves will deposit their negative momentum to the large-scale flow, and accelerate the large-scale zonal flow westward in the region where the diffusion or breaking of the gravity waves exist. As a result, the easterly zonal mean flow in the winter stratosphere in January and November may be due to the deposition of gravity wave momentum to the large-scale zonal flow. Non-zero vertical gradient of zonal and meridional momentum flux in January and November can be clearly seen in the vertical profiles of monthly mean zonal and meridional momentum fluxes in the stratosphere. In January, the magnitude of the zonal momentum flux above z = 20.5 km decreases with the altitude, and approaches to zero above z = 28 km. In November, the magnitude of zonal momentum flux decrease rapidly with height in the altitude range between z = 19.5 km and 22 km. This vertical structure of the zonal momentum flux in the winter stratosphere indicates that the gravity waves can accelerate the large-scale zonal wind westward.

Previous: Observation and data analysis Next: Summary Up:Ext. Abst.