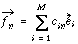 .
.
Each element  corresponds to the coefficient associated with the ith eigenvector
for the nth observation. As Kutzbach (1967) points out, "the coefficients
corresponds to the coefficient associated with the ith eigenvector
for the nth observation. As Kutzbach (1967) points out, "the coefficients
 play the same role in See .. as the coefficients in ... a Fourier series."
play the same role in See .. as the coefficients in ... a Fourier series."
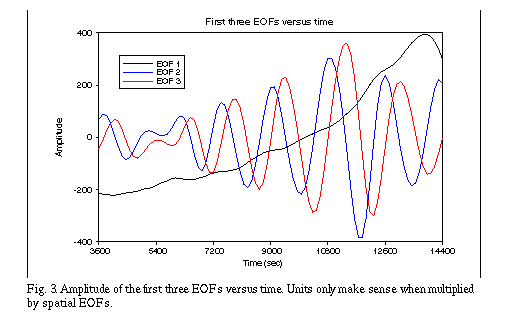
We calculated EOFs for the perturbation horizontal and vertical
velocity and potential temperature fields of the simulation at
times ranging from 3600 to 14400 seconds. Here, perturbations
are defined as deviations from the initial horizontal mean. To
normalize the potential temperature perturbations and convert
them to velocity units, they were multiplied by 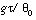 , where
, where 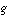 is the acceleration of gravity,
is the acceleration of gravity, 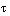 is a Brunt-Väisälä time scale of 100 s and
is a Brunt-Väisälä time scale of 100 s and 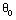 is the vertically-varying basic-state potential temperature.
Since the calculation of EOFs is extremely memory-intensive, we
had to calculate the EOFs at points that covered a limited portion
of the domain (from -200 km to +200 km in the horizontal), and
with limited resolution (every 4 km in the horizontal and every
1.25 km in the vertical.) With output fields saved every 120 seconds,
this made for 91 "observations" at each point. A plot of the time-varying
coefficients for the first five EOFs is shown in Fig. 3.
is the vertically-varying basic-state potential temperature.
Since the calculation of EOFs is extremely memory-intensive, we
had to calculate the EOFs at points that covered a limited portion
of the domain (from -200 km to +200 km in the horizontal), and
with limited resolution (every 4 km in the horizontal and every
1.25 km in the vertical.) With output fields saved every 120 seconds,
this made for 91 "observations" at each point. A plot of the time-varying
coefficients for the first five EOFs is shown in Fig. 3.
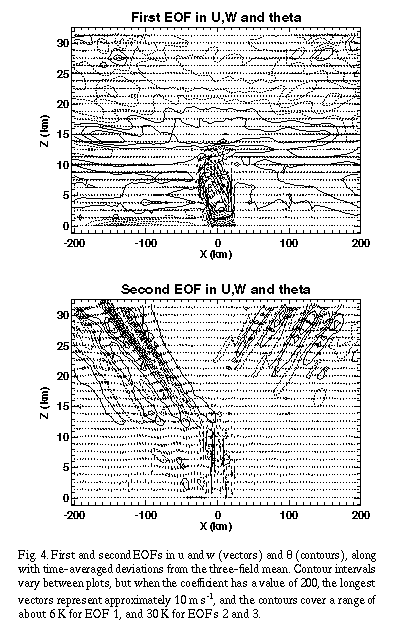
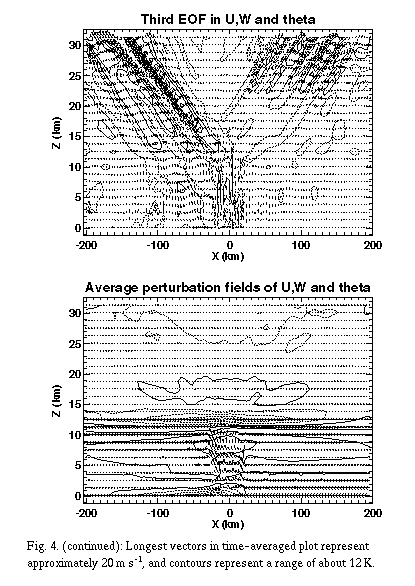
The spatial structures of the first three EOFs in u, w and ¸ are
shown in Fig. 4. The first EOF (containing 12% of the variance)
seems to be associated with the strengthening of the convection,
due to its similarity in structure to the storm averaged perturbations,
and its nearly monotonic increase in amplitude. The second and
third EOFs (containing 7% of the variance apiece) are very similar
(but slightly out of phase) in spatial and temporal structure.
They have most of their amplitude in the stratosphere (apart from
some large velocity perturbations near the region of convection),
and exhibit a phase relationship indicative of outward-propagating
gravity waves, as explained below. When the second and third EOFs
are combined in space and time (not shown), the combined mode
is similar in structure to the individual modes, except with higher
amplitude.
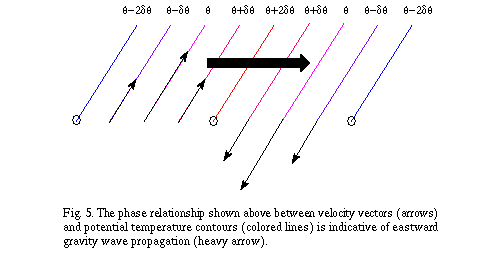
The direction that the waves in EOFs 2 and 3 are propagating can
be ascertained by examining the relative phase of vertical velocity
and potential temperature. A simplified depiction of one of these
waves is shown in Fig 5. On the left side of this wave, the upward
motion causes the air to cool, while the downward motion on the
right side of the wave is associated with warming. Since the coldest
and warmest air is to the left of the peak cooling and warming,
respectively, the wave propagates to the right.
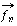 represent a vector of observations at M different spatial locations
taken at the nth time. If we are examining N times at which observations
are taken, then F is an M by N matrix, with the nth column corresponding
to
represent a vector of observations at M different spatial locations
taken at the nth time. If we are examining N times at which observations
are taken, then F is an M by N matrix, with the nth column corresponding
to 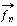 . We are looking for the vector
. We are looking for the vector 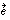 that is most similar to all of the
that is most similar to all of the 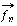 simultaneously. The way that Kutzbach (1967) measures similarity
is by taking the normalized, squared inner product between
simultaneously. The way that Kutzbach (1967) measures similarity
is by taking the normalized, squared inner product between 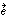 and F:
and F: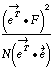 .
.
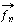 can be expanded as a sum of eigenvectors given by
can be expanded as a sum of eigenvectors given by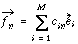 .
.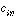 corresponds to the coefficient associated with the ith eigenvector
for the nth observation. As Kutzbach (1967) points out, "the coefficients
corresponds to the coefficient associated with the ith eigenvector
for the nth observation. As Kutzbach (1967) points out, "the coefficients
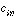 play the same role in
play the same role in 
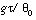 , where
, where 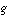 is the acceleration of gravity,
is the acceleration of gravity, 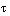 is a Brunt-Väisälä time scale of 100 s and
is a Brunt-Väisälä time scale of 100 s and 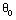 is the vertically-varying basic-state potential temperature.
Since the calculation of EOFs is extremely memory-intensive, we
had to calculate the EOFs at points that covered a limited portion
of the domain (from -200 km to +200 km in the horizontal), and
with limited resolution (every 4 km in the horizontal and every
1.25 km in the vertical.) With output fields saved every 120 seconds,
this made for 91 "observations" at each point. A plot of the time-varying
coefficients for the first five EOFs is shown in Fig. 3.
is the vertically-varying basic-state potential temperature.
Since the calculation of EOFs is extremely memory-intensive, we
had to calculate the EOFs at points that covered a limited portion
of the domain (from -200 km to +200 km in the horizontal), and
with limited resolution (every 4 km in the horizontal and every
1.25 km in the vertical.) With output fields saved every 120 seconds,
this made for 91 "observations" at each point. A plot of the time-varying
coefficients for the first five EOFs is shown in Fig. 3.