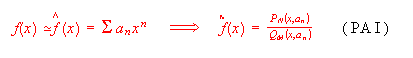
| Home | Institutes | Experiments | Miscellaneous |Physics Today for Physics Tomorrow|
| My CV | List of publications |
Interpolation - extrapolation by Padé Approximants
Florian Nichitiu
This method is based on the extension of the second type Padé approximant (PA) to rational fraction least squares minimization. The method can be used to approximate real as well as analytic functions which are complex on the real axis, can be applied to a large spectrum of problems and has been successfully applied for resonance search in partial wave analysis.
In contrast to PA of type I which are the ratio of two polynomials of degree N and M constructed from the given coefficients of the Taylor series of the function to be approximated :
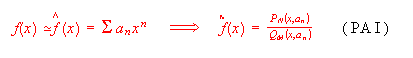
the second type PA uses for its construction a set of function values at a given number of points. Therefore, PA II which has been classically called the Cauchy interpolation, is the pointwise interpolation by polynomial rational functions:
![]()
Our approach consists in using the PA II in order to construct the best representation of the function with a subsequent improvement by the least squares minimization and where the functions used to construct the PA II are taken just as free parameters.
For general case, the problem is to approximate an analytic function F(x) which is complex on the real axis.
![]()
by using N given values of it :
![]()
The approximant of F(x) is therefore :
![]()
If we define :
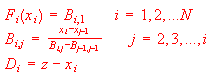
The approximant will be given by :
![]()
where P and Q are given by the recurrence formula :
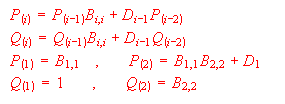
This approximant is in fact a ratio of two polynomials of degree n and m :
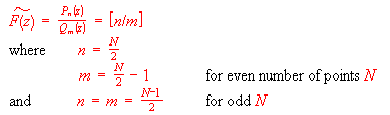
This method for constructing the approximant of an analytic complex function is straight forward to use and is flexible because the input data points are arbitrary and can be chosen to best represent the function.
A subsequent improvement is achieved by least squares minimization using as free parameters the function values used already in Padé construction of second type::
![]()
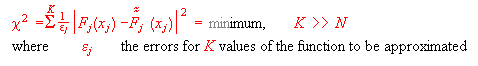
We shall call the newly obtained approximant the Padé approximant of third type (PA III):
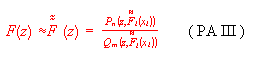
In practice, the direct fit of the data with a rational fraction is not easy to be performed because of the no linearity of the minimization problem and, as usual the convergence is very slowly. In our procedure the convergence is very fast, and well interpolate and extrapolate the given function even in the case when the initial PA II badly approximate the function.
| Home | Institutes | Experiments | Miscellaneous |Physics Today for Physics Tomorrow|
| My CV | List of publications |