
|
Dr. Gordan R. Stuhne
Atmospheric Physics Group, Room MP609
Department of Physics, University of Toronto
60 St. George Street, Toronto, ON, Canada M5S 1A7
Phone: (416) 946-3019
Index
|
Atmospheric Physics Home
Home
Image Gallery

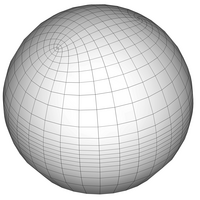
Structured (orthogonal tripolar) vs. unstructured
(icosahedral quadtree) spherical grids.
|
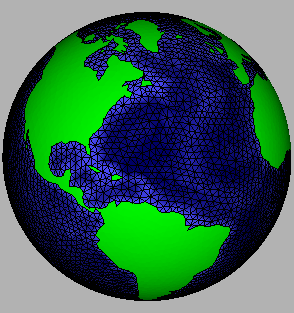
World ocean bathymetry contoured on
coastally conforming unstructured triangular grid.
|
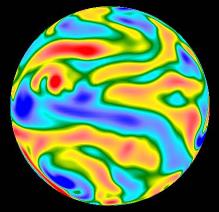
Jet formation in decaying shallow water turbulence.
|
|
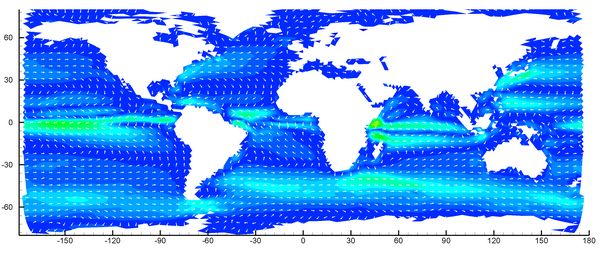
World ocean circulation in an unstructured grid model
(projected into latitude-longitude coordinates).
|
Home
Research Interests
Background
My research interests relate to the
computational modeling of complex hydrodynamic
systems. At present, I am engaged in
the development of numerical techniques for
oceanic and climatological simulation, but I
have also worked in biophysical and biomedical
application areas. A key challenge in
all of these fields is the formulation
and implementation of continuum-mechanical
models of systems whose detailed, small-scale
behavior is complex and unpredictable.
My specific contributions (with various
collaborators) and ongoing work are given, in point form,
below, followed by a
list of publications.
To try to explain the overall motivation and
theme, I will begin with this general discussion,
for which literature references may be found
in the listed publications.
Hydrodynamic equations express the continuous
forms of the conservation laws for momentum and
a variety of other physical quantities (e.g.,
internal energy, or the salt content of the ocean). These
laws are statistical in the sense that they apply
to the bulk properties of materials whose
microscale behavior is not taken into account.
In Eulerian terms, each quantity is assumed to be
advected by a local mean current as it is scattered
by random (i.e., unknown) fluctuations, which induce
diffusion. Allowing also for sources and sinks, the
redistribution of a scalar quantity,
C, in space is governed by the conservation equation,
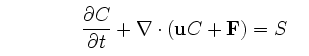
in which the local
advecting velocity, u, itself evolves
(nonlinearly) through time on account of an analogous
redistribution of vector momentum. The form of the
diffusive flux, F, depends upon the
probability distribution of deviations from the
mean motion, with the assumption of an isotropic
random walk leading, for example, to the standard
Fickian counter-gradient diffusion law: i.e.,
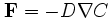 .
.
General Areas of Interest
The application of hydrodynamical approximation
to molecular systems yields the well-studied
Navier-Stokes
equations, which are known to provide a very good
description of fluids in most situations.
Outstanding research issues at this level mostly
relate to mesh generation and geometric
transformation techniques for representing
complex spatial domains in computational models,
as well as to the formulation of discretizations
that offer optimal accuracy while preserving
fundamental hydrodynamical conservation laws.
When one considers complex fluid systems like the
ocean or atmosphere, naive numerical solution of the
Navier-Stokes equations is totally impractical.
Instead, hydrodynamical reasoning is applied to
a succession of models, with the high-frequency
or eddy motions occurring in one model being
identified with the randomizing mechanism in a less
complete, but more useful, simplified model. There
are a variety of well-known chains of approximation:
e.g., in geophysical fluid dynamics,
compressible -> anelastic -> Boussinesq;
non-hydrostatic -> hydrostatic -> shallow-water;
ageostrophic -> geostrophic -> nondivergent barotropic,
etc. These chains often run perpendicular to
each other and link together into a network
of related models. As one traverses this network,
the basic conservation structure of the Navier-Stokes
equations remains essentially unchanged, but
ad hoc assumptions are typically made about the
diffusive fluxes with the aim of mimicking
physics that is unresolved with a given hydrodynamical
approximation and computational grid.
Finding convincing a priori mathematical justifications for
such parameterizations is very difficult, and
most research in this area boils down to the
discretization of different hydrodynamical models
and parameterization schemes, and to the comparison
of simulation results with each other and with
empirical data. In this context, it is of interest
to understand the relationships amongst different
models and parameterizations at the level of the
computational algorithms, and to systematize
comparisons amongst their various predictions.
Finally, there is an interesting class of situations
in which hydrodynamic reasoning can be applied
fairly rigorously, but with inaccurate or
counter-intuitive results. For example, if
one aims to model the concentration of biological
organisms like marine plankton, it can be proven
mathematically that there are important cases where
the continuous hydrodynamic quantity is strictly diffused,
even though the discrete population dynamics results
in the formation of spatially localized clusters (an
inherently non-diffusive phenomenon). The inaccuracy
of the hydrodynamic approximation results because
there are large non-conservative statistical fluctuations
in the local concentration field. Any introduction
of biological components into hydrodynamic models
must hence be at the level of the carbon cycle and/or
other dynamical processes involving precise conservation
laws. In a related vein, the nonlinear self-advection
entailed in the momentum conservation law complicates
the simplistic association of "eddies" with random
mixing and diffusion. This is exemplified by the way
in which coherent large-scale vortices and banded zonal
flows can sometimes be generated, rather than dissipated,
by unordered small-scale turbulence - an important
phenomenon that may account
for the observed structures of the atmospheres of
the gaseous giant planets, and for the complex bands
in the Antarctic circumpolar ocean current.
Asymptotic analyses of so-called Kolmogorov flows
(which represent a very simple idealized case) capture
aspects of such anti-diffusive dynamics, which appear
when the derived large-scale diffusion coefficient
becomes negative. Studying oddities of this kind
helps build understanding of the assumptions (and potential
pitfalls) inherent in any application of hydrodynamical
approximation.
Specific Topics
- novel discretizations for hydrostatic Boussinesq
and swallow water equations and other geophysical
models on
unstructured spherical triangular grids
- staggered finite-volume/finite-difference methods
that enforce both linear and quadratic conservation
properties
- implicit time-stepping methods that maintain
discrete conservation over the time domain
- Cartesian discretization methods
that optimize spatial accuracy on local spherical patches
- computational mesh generation and geometry
- block-structured, quadtree, and advancing
front mesh generation techniques for triangulating
the global ocean and atmosphere
- terrain-following z-coordinate transformations
for unstructured spherical grids
- mesh cutting and mesh searching methods relating to
virtual endovascular surgery and virtual ultrasound
- other topics in hydrodynamic modeling
- mixing parameterizations for global ocean models
- non-hydrodynamic clustering resulting from
marine plankton population dynamics
- jet formation in shallow-water and nondivergent
barotropic turbulence; Kolmogorov flows
- advection, diffusion and sedimentation
of angiographic contrast medium for virtual angiography
Home
Publications
Refereed Journals and Book Chapters
- Stuhne, G. R., Peltier, W. R. (2006) A Robust
Unstructured Grid Discretization for 3-Dimensional
Hydrostatic Flows in Spherical Geometry: A New
Numerical Structure for Ocean General Circulation
Modeling.
Journal of Computational Physics 213 (2) 704-729.
[DOI]
- Ford M. D., Stuhne G. R., Nikolov H. N., Habets D. F., Lownie S. P.,
Holdsworth D. W., Steinman D. A. (2005)
Virtual Angiography for Visualization and Validation
of Computational Models of Aneurysm Hemodynamics.
IEEE Trans Med Imaging 24 (12) 1586-1592.
[DOI]
- Stuhne, G. R., Steinman, D. A. (2004) Finite-element
modeling of the hemodynamics of stented aneurysms.
Journal of Biomechanical Engineering-Transactions of
the ASME 126 (3) 382-387.
[DOI]
- Khoshniat, M., Stuhne, G. R., Steinman, D. A. (2003)
Relative performance of geometric search algorithms for
interpolating unstructured mesh data.
Medical Image Computing and Computer-assisted
Intervention - MICCAI 2003, pt 2 2879,
391-398.
Book series title: Lecture Notes in Computer Science
[DOI]
- Peltier, W. R., Stuhne, G. R. (2002) The Upscale Turbulent
Cascade: Shear Layers, Cyclones and Gas Giant Bands.
In Meteorology at the Millenium, R. P. Pierce, ed.,
Academic Press, San Diego.
- Young, W. R., Roberts, A. J., Stuhne, G. (2001)
Reproductive pair correlations and the clustering of
organisms.
Nature 412 (6844): 328-331.
[DOI]
- Stuhne, G. R. (2001) One-dimensional dynamics of
zonal jets on rapidly rotating spherical shells.
Physica D 149(1-2): 43-79.
[DOI]
- Stuhne, G. R., Peltier, W. R. (1999) New icosahedral
grid-point discretizations of the shallow water equations
on the sphere.
Journal of Computational Physics 148 (1): 23-58.
[DOI]
- Stuhne, G. R., Peltier, W. R. (1996) Vortex erosion and
amalgamation in a new model of large scale flow on the sphere.
Journal of Computational Physics 128 (1): 58-81.
[DOI]
Invited Talks
- Apr. 2006. "Computational design of a new
unstructured grid model of the world ocean circulation."
(with W. R. Peltier)
To be presented at the General Assembly of the European
Geosciences Union. Vienna, Austria.
- Nov. 2005. "A Conservative Discretization for Hydrodynamics
on the Sphere: Simulating Global Ocean Dynamics on Unstructured Grids."
University of Waterloo Computational Mathematics Colloquium.
Waterloo, Ontario [abstract].
- Nov. 2005. "Conservative Unstructured Grid Methods for Global Ocean
Modelling."
TAO Seminar Series (Topics in the Atmosphere and Ocean).
Canadian Centre for Climate Modelling and Analysis (CCCMA) and
the School of Earth and Ocean Sciences (SEOS).
Victoria, British Columbia [link].
- Dec. 2000. "Reduced Hydrodynamic Models of Structure
Formation in Rotating Spherical Flows."
AGU Fall meeting, San Fancisco, California.
Eos Trans. AGU
81 (48), Abstract NG61A-10.
- Mar. 1999. "Decaying Shallow Water Turbulence on the Rotating Sphere: Numerical
Simulations of Eddy/Mean Flow Interaction."
Geophysical Fluid Dynamics Laboratory (GFDL) Seminar.
Princeton, New Jersey [link].
Conference Proceedings
- Stuhne, G. R. and W. R. Peltier.
"Unstructured Grid Techniques for Global Ocean Modeling and Prediction."
Accepted for ASLO/ERF/TOS/AGU Ocean Sciences Meeting,
Honolulu, Hawaii, February 2006. Eos Trans. AGU
87 (36) (2006), Abstract OS26O-12.
- Ford, M. D., G. R. Stuhne, H. N. Nikolov, S. P. Lownie, D. W.
Holdsworth, and D. A. Steinman.
"Virtual angiography for visualization and
validation of computational fluid dynamics models of aneurysm hemodynamics."
Proceedings of the SPIE Medical Imaging Conference.
San Diego, California. February 2005 [link].
- Stuhne, G. R. and W. R. Peltier.
"A new global model of the general circulation of
the oceans: experiments with variable spatial resolution on
unstructured grids." Poster presentation.
IAPSO/SCOR Ocean Mixing Conference.
Victoria, British Columbia. October 2004.
-
Stuhne, G. R. and D. A. Steinman.
"Mesh resolution requirements for the numerical simulation of flow
through stented aneurysms."
Proceedings of the ASME Bioengineering Conference.
Key Biscayne, Florida. June 2003.
-
Stuhne, G. R. and W. R. Peltier.
"Barotropic and Shallow Water Dynamics in a New Spherical,
Icosahedral, Grid-Point Model."
Presented at the Conference on Mathematical Geophysics, Cambridge,
U. K., July 1998.
J. Conf. Abs.
3 (1998): 25 [abstract].
-
Stuhne, G. R. and W. R. Peltier.
"Shallow Water Experiments with a Spherical Icosahedron-Based
Multigrid Model."
Presented at the 23rd General Assembly of the European
Geophysical Society, Nice, France, April 1998.
Annales Geophysicae
16 (suppl. IV) (1998): 1136 [link].
-
Stuhne, G. R. and W. R. Peltier.
"On the Dynamics of Unstable Zonal Jets and Coherent Spots in a New
Spherical Grid-Point Model."
Proceedings of the Joint Assemblies of the International
Association of Meteorology and Atmospheric Sciences & International
Association for Physical Sciences of the Oceans.
Melbourne, Australia. July 1997.
-
Stuhne, G. R. and W. R. Peltier.
"Spherical Hydrodynamics in a New Icosahedral Grid-Point Model."
Proceedings of the Joint Workshops on Numerical Methods for
Global Models.
Breckenridge, Colorado. June 1996.
-
Stuhne, G. R. and W. R. Peltier.
"Vortex Erosion and Amalgamation in 2-D Turbulence on the Sphere: A
New Model Based Upon an Icosahedral Discretization."
Presented at the 21st General Assembly of the European
Geophysical Society, The Hague, Netherlands, May 1996.
Annales Geophysicae
14 (suppl. II) (1996): 669.
-
Stuhne, G. R. and W. R. Peltier.
"Vortex Erosion and Amalgamation in a New Model of Large-Scale Flow
on the Sphere."
Proceedings of the Tenth Conference on Atmospheric and
Oceanic Waves and Stability.
Big Sky, Montana. June 1995.





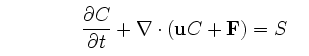
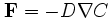 .
.